Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T18:17:42.545Z Has data issue: false hasContentIssue false
  • English
  • Français

Dependent Automorphisms in Prime Rings

Published online by Cambridge University Press:  20 November 2018

Matej Brešar ,
W. S. Martindale 3rd  and
C. Robert Miers
Matej Brešar
Affiliation:
University of Maribor PF, Koroška 160 62000 Maribor Slovenia
W. S. Martindale 3rd
Affiliation:
Department of Mathematics University of Massachusetts Amherst, MA 01003 USA
C. Robert Miers
Affiliation:
Department of Mathematics and Statistics University of Victoria Victoria, BC V8W 3P4
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For each 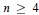$n\ge 4$ we construct a class of examples of a minimal 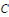$C$-dependent set of $n$ automorphisms of a prime ring 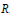$R$, where 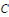$C$ is the extended centroid of 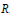$R$. For 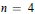$n=4$ and 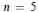$n=5$ it is shown that the preceding examples are completely general, whereas for 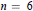$n=6$ an example is given which fails to enjoy any of the nice properties of the above example.

Keywords

16N6016W20
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 41 , Issue 4 , 01 December 1998 , pp. 452 - 462
Copyright
Copyright © Canadian Mathematical Society 1998

References

[A] Batty, C. J. K., On certain pairs of automorphisms of C*-algebras. J. Austral. Math. Soc. 46 (1989), 197–211.Google Scholar
[B] Beidar, K. I., Martindale, W. S. III and Mikhalev, A. V., Rings with Generalized Identities. Marcel Dekker, 1995.Google Scholar
[C] Brešar, M., On certain pairs of automorphisms of rings, II. Preprint.Google Scholar
[D] Martindale, W. S. III and Susan Montgomery, The normal closure of coproducts of domains. J. Algebra 82 (1983), 1–17.Google Scholar