Demonstration de la Formule Künneth par la Theorie Harmonique

Extract

Etant données deux variétés différentiables compactes M et N, nous avons la formule de Künneth

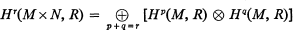
qui établit la relation entre la cohomologie réelle de la variété produit avec celle des facteurs. Cette formule est bien connue en topologie algébrique, et elle est valable dans le contexte plus général de la catégorie des espaces topologiques. Nous voulons donner ici une démonstration de cette formule par la théorie harmonique de Hodge-Kodaira [1]. Une telle démonstration n'est pas explicite, autant que je sache, dans la littérature; elle est désirable, par exemple, dans un cours de géométrie différentielle sur les formes harmoniques.