No CrossRef data available.
Published online by Cambridge University Press: 22 November 2022
We study the following decision problem: given an exponential equation  $a_1g_1^{x_1}a_2g_2^{x_2}\dots a_ng_n^{x_n}=1$ over a recursively presented group G, decide if it has a solution with all
$a_1g_1^{x_1}a_2g_2^{x_2}\dots a_ng_n^{x_n}=1$ over a recursively presented group G, decide if it has a solution with all 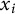 $x_i$ in
$x_i$ in 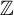 $\mathbb {Z}$. We construct a finitely presented group G where this problem is decidable for equations with one variable and is undecidable for equations with two variables. We also study functions estimating possible solutions of such an equation through the lengths of its coefficients with respect to a given generating set of G. Another result concerns Turing degrees of some natural fragments of the above problem.
$\mathbb {Z}$. We construct a finitely presented group G where this problem is decidable for equations with one variable and is undecidable for equations with two variables. We also study functions estimating possible solutions of such an equation through the lengths of its coefficients with respect to a given generating set of G. Another result concerns Turing degrees of some natural fragments of the above problem.