Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T01:25:19.893Z Has data issue: false hasContentIssue false
  • English
  • Français

Cubic Functional Equations on Restricted Domains of Lebesgue Measure Zero

Published online by Cambridge University Press:  20 November 2018

Chang-Kwon Choi ,
Jaeyoung Chung ,
Yumin Ju  and
John Rassias
Chang-Kwon Choi
Affiliation:
Department of Mathematics, Jeonbuk National University, Jeonju þ@Ë-6þ@, Republic of Korea e-mail: [email protected]
Jaeyoung Chung
Affiliation:
Department of Mathematics, Kunsan National University, Kunsan þ6h-6§Ë, Republic of Korea e-mail: [email protected] [email protected]
Yumin Ju
Affiliation:
National and Capodistrian University of Athens, Pedagogical Department E. E., Athens, Greece e-mail: [email protected]
John Rassias
Affiliation:
Department of Mathematics, Kunsan National University, Kunsan þ6h-6§Ë, Republic of Korea e-mail: [email protected] [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

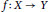Let $X$ be a real normed space, $Y$ a Banach space, and $f\,:\,X\,\to \,Y$. We prove theUlam–Hyers stability theorem for the cubic functional equation

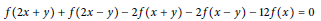$$f\left( 2x\,+\,y \right)\,+\,f\left( 2x\,-\,y \right)\,-\,2f\left( x\,+\,y \right)\,-\,2f\left( x\,-\,y \right)\,-\,12f\left( x \right)\,=\,0$$

in restricted domains. As an application we consider a measure zero stability problem of the inequality

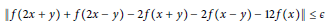$$\left\| f\left( 2x\,+\,y \right)\,+\,f\left( 2x\,-\,y \right)\,-\,2f\left( x\,+\,y \right)\,-\,2f\left( x\,-\,y \right)\,-\,12f\left( x \right) \right\|\,\le \,\varepsilon$$

for all 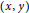$\left( x,\,y \right)$ in 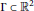$\Gamma \,\subset \,{{\mathbb{R}}^{2}}$ of Lebesgue measure 0.

Keywords

39B82Baire category theoremcubic functional equationfirst categoryLebesgue measureUlam-Hyers stability
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 1 , 01 March 2017 , pp. 95 - 103
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Alsina, C. and Garcia-Roig, J. L., On a conditional Cauchy equation on rhombuses. In: Functional analysis, approximation theory and numerical analysis, World Scientific, River Edge, NJ, 1994.Google Scholar
[2] Batko, B., Stability of an alternative functional equation. J. Math. Anal. Appl. 339(2008), no. 1, 303–311. http://dx.doi.Org/10.101 6/j.jmaa.2007.07.001 Google Scholar
[3] Batko, B., On approximation of approximate solutions ofDhombres’ equation. J. Math. Anal. Appl. 340(2008), no. 1, 424–432. http://dx.doi.Org/10.101 6/j.jmaa.2007.08.009 Google Scholar
[4] Brzdek, J., On the quotient stability of a family of functional equations. Nonlinear Anal. 71(2009), no. 10, 4396–4404. http://dx.doi.Org/10.1016/j.na.2009.02.123 Google Scholar
[5] Brzdek, J., On a method of proving the Hyers-Ulam stability of functional equations on restricted domains. Aust. J. Math. Anal. Appl. 6(2009), 1–10.Google Scholar
[6] Bahyrycz, A. and Brzdek, J., On solutions of the d'Alembert equation on a restricted domain. Aequationes Math. 85(2013), no. 1-2, 169–183. http://dx.doi.Org/10.1007/s00010-012-0162-x Google Scholar
[7] Brzdçk, J. and Sikorska, J., A conditional exponential functional equation and its stability. Nonlinear Anal. 72(2010), no. 6, 2923–2934. http://dx.doi.Org/10.101 6/j.na.2009.11.036 Google Scholar
[8] Chung, J., Stability of functional equations on restricted domains in a group and their asymptotic behaviors. Comput. Math. Appl. 60(2010), no. 9, 2653–2665. http://dx.doi.Org/1 0.101 6/j.camwa.2O10.09.003 Google Scholar
[9] Chung, J. and Rassias, J. M., Quadratic functional equations in a set of Lebesgue measure zero. J. Math. Anal. Appl. 419(2014), no. 2, 1065–1075. http://dx.doi.Org/10.101 6/j.jmaa.2O14.05.032 Google Scholar
[10] Ger, R. and Sikorska, J., On the Cauchy equation on spheres. Ann. Math. Sil. 11(1997), 89–99.Google Scholar
[11] Hyers, D. H., On the stability of the linear functional equations. Proc. Nat. Acad. Sci. USA 27(1941), 222–224. http://dx.doi.Org/10.1073/pnas.27.4.222 Google Scholar
[12] Jun, K.-W. and Kim, H.-M., The generalized Hyers-Ulam-Rassias stability of a cubic functional equation. J. Math. Anal. Appl. 274(2002), no. 2, 867–878. http://dx.doi.Org/10.1016/S0022-247X(02)00415-8 Google Scholar
[13] Jung, S.-M., Hyers-Ulam-Rassias stability of functional equations in nonlinear analysis. Springer Optimization and Its Applications, 48, Springer, New York, 2011. http://dx.doi.Org/10.1007/978-1-4419-9637-4 Google Scholar
[14] Jung, S.-M., On the Hyers-Ulam stability of the functional equations that have the quadratic property. J. Math. Anal. Appl. 222(1998), no. 1, 126–137. http://dx.doi.Org/1 0.1006/jmaa.1 998.591 6 Google Scholar
[15] Kuczma, M., Functional Equations on restricted domains. Aequationes Math. 18(1978), no. 1-2, 1–34. http://dx.doi.Org/10.1007/BF01844065 Google Scholar
[16] Oxtoby, J. C., Measure and category. Graduate Texts in Mathematics, 2, Springer-Verlag, New York, 1980.Google Scholar
[17] Rassias, J. M. and Rassias, M. J., On the Ulam stability of Jensen and Jensen type mappings on restricted domains. J. Math. Anal. Appl. 281(2003), no. 2, 516–524. http://dx.doi.Org/10.1016/S0022-247X(03)00136-7 Google Scholar
[18] Rassias, J. M., On the Ulam stability of mixed type mappings on restricted domains. J. Math. Anal. Appl. 281(2002), no. 2, 747–762. http://dx.doi.Org/10.101 6/S0022-247X(02)00439-0 Google Scholar
[19] Sikorska, J., On two conditional Vexider functional equations and their stabilities. Nonlinear Anal. 70(2009), no. 7, 2673–2684. http://dx.doi.Org/10.1016/j.na.2008.03.054 Google Scholar
[20] Skof, F., Sull'approssimazione dette applicazioni localmente S-additive. Atii Accad. Sci. Torino Cl. Sci. Fis. Mat. Natur. 117(1983), no. 4-6, 377–389.Google Scholar