Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-13T08:51:57.235Z Has data issue: false hasContentIssue false
  • English
  • Français

Covering the Unit Sphere of Certain Banach Spaces by Sequences of Slices and Balls

Published online by Cambridge University Press:  20 November 2018

Vladimir P. Fonf  and
Clemente Zanco
Vladimir P. Fonf
Affiliation:
Department of Mathematics, Ben-Gurion University of the Negev, 84105 Beer-Sheva, Israel e-mail: [email protected]
Clemente Zanco
Affiliation:
Dipartimento di Matematica, Università degli Studi, Via C. Saldini, 50, 20133 Milano MI, Italy e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that, given any covering of any infinite-dimensional Hilbert space 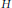$H$ by countably many closed balls, some point exists in 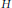$H$ which belongs to infinitely many balls. We do that by characterizing isomorphically polyhedral separable Banach spaces as those whose unit sphere admits a point-finite covering by the union of countably many slices of the unit ball.

Keywords

46B2046C0552C17point finite coveringsslicespolyhedral spacesHilbert spaces
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 1 , 14 March 2014 , pp. 42 - 50
Copyright
Copyright © Canadian Mathematical Society 2014

References

[Co] Corson, H. H., Collections of convex sets which cover a Banach space. Fund. Math. 49 (1961), 143–145.Google Scholar
[FL] Fonf, V. P. and Lindenstrauss, J., Some results on infinite-dimensional convexity. Israel J. Math. 108 (1998), 13–32. http://dx.doi.org/10.1007/BF02783039 Google Scholar
[Fo1] Fonf, V. P., Polyhedral Banach spaces. Math. Notes 30 (1981), 809–813.Google Scholar
[Fo2] Fonf, V. P., Three characterizations of polyhedral Banach spaces. Ukrainian Math. J. 42 (1990), 1286–1290.Google Scholar
[FR] Fonf, V. P. and Rubin, M., A reconstruction theorem for homeomorphism groups without small setsand non-shrinking functions of a normed space. In preparation.Google Scholar
[FZ1] Fonf, V. P. and Zanco, C., Covering a Banach space. Proc. Amer. Math. Soc. 134 (2004), 2607–2611. http://dx.doi.org/10.1090/S0002-9939-06-08254-2 Google Scholar
[FZ2] Fonf, V. P. and Zanco, C., Finitely locally finite coverings of Banach spaces. J. Math. Anal. Appl. 350 (2009), 640–650. http://dx.doi.org/10.1016/j.jmaa.2008.04.071 Google Scholar
[FZ3] Fonf, V. P. and Zanco, C., Coverings of Banach spaces: beyond the Corson theorem. Forum Math. 21 (2009), 533–546. http://dx.doi.org/10.1515/FORUM.2009.026 Google Scholar
[FZ4] Fonf, V. P. and Zanco, C., Covering spheres of Banach spaces by balls. Math. Ann. 344 (2009), 939–945. http://dx.doi.org/10.1007/s00208-009-0336-6 Google Scholar
[JL] Johnson, W. B. and Lindenstrauss, J., Basic Concepts in the Geometry of Banach Spaces. In: Handbook of the Geometry of Banach Spaces Vol. 1, North-Holland, Amsterdam, 2001, 1–84.Google Scholar
[Kl1] Klee, V., Polyhedral sections of convex bodies. Acta Math. 103 (1960), 243–267. http://dx.doi.org/10.1007/BF02546358 Google Scholar
[Kl2] Klee, V., Dispersed Chebyshev sets and covering by balls. Math. Ann. 257 (1981), 251–260. http://dx.doi.org/10.1007/BF01458288 Google Scholar
[MZ] Marchese, A. and Zanco, C., On a question by Corson about point-finite coverings. Israel J. Math. 189 (2012), 55–63. http://dx.doi.org/10.1007/s11856-011-0126-1 Google Scholar
[Pa] Papini, P. L., Covering the sphere and the ball in Banach spaces. Commun. Appl. Anal. 13 (2009), 579–586.Google Scholar