Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-20T10:29:09.806Z Has data issue: false hasContentIssue false
  • English
  • Français

Covering Discs in Minkowski Planes

Published online by Cambridge University Press:  20 November 2018

Horst Martini  and
Margarita Spirova
Horst Martini
Affiliation:
Fakultät für Mathematik, TU Chemnitz, D-09107 Chemnitz, Germany e-mail: [email protected]
Margarita Spirova
Affiliation:
Faculty of Mathematics and Informatics, University of Sofia, 5 James Bourchier, 1164 Sofia, Bulgaria e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate the following version of the circle covering problem in strictly convex (normed or) Minkowski planes: to cover a circle of largest possible diameter by $k$ unit circles. In particular, we study the cases 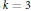$k\,=\,3$, 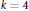$k\,=\,4$, and 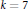$k\,=\,7$. For 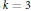$k\,=\,3$ and 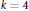$k\,=\,4$, the diameters under consideration are described in terms of side-lengths and circumradii of certain inscribed regular triangles or quadrangles. This yields also simple explanations of geometric meanings that the corresponding homothety ratios have. It turns out that basic notions from Minkowski geometry play an essential role in our proofs, namely Minkowskian bisectors, $d$-segments, and the monotonicity lemma.

Keywords

46B2052A2152C15affine regular polygonbisectorcircle covering problemcircumradiusd-segmentMinkowski plane(strictly convex) normed plane
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 52 , Issue 3 , 01 September 2009 , pp. 424 - 434
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Asplund, E. and Grünbaum, B., On the geometry of Minkowski planes. Enseignement Math. 6(1960), 299–306.Google Scholar
[2] Bezdek, K., Über einige Kreisüberdeckungen. Beiträge Algebra Geom. 14(1983), 7–13.Google Scholar
[3] Bezdek, K., Über einige optimale Konfigurationen von Kreisen. Ann. Univ. Sci. Bedapest Eötvös Sect. Math. 27(1984), 143–151.Google Scholar
[4] Boltyanski, V., Martini, H., and Soltan, P. S., Excursions into Combinatorial Geometry. Springer-Verlag, Berlin, 1996.Google Scholar
[5] Böröczky, K. Jr., Finite Packing and Covering. Cambridge Tracts in Mathematics 154, Cambridge University Press, 2004.Google Scholar
[6] Fejes Tóth, G., Packing and covering. In: Handbook of Discrete and Computational Geometry. CRC Press, Ser. Discrete Math. Appl., Boca Raton, FL, 1997, Ch. 2.Google Scholar
[7] Fejes Tóth, G., Thinnest covering of a circle by eight, nine or ten circles. In: Combinatorial and Computational Geometry. Math. Sci. Res. Inst. Publ. 52, Cambridge University Press, 2005, pp. 361–376.Google Scholar
[8] Grünbaum, B., On a conjecture of H. Hadwiger. Pacific J. Math. 11(1961), 215–219.Google Scholar
[9] Hadwiger, H., Über Treffanzahlen bei translationsgleichen Eikörpern. Arch. Math. 8(1957), 212–213.Google Scholar
[10] Heppes, A., Covering a planar domain with sets of small diameters. Period. Math. Hungar. 53(2006), no. 1-2, 157–168.Google Scholar
[11] Holub, J. R., Rotundity, orthogonality, and characterizations of inner product spaces. Bull. Amer. Math. Soc. 81(1975), 1087–1089.Google Scholar
[12] Lassak, M., Covering a plane convex body by four homothetical copies with the smallest positive ratio. Geom. Dedicata 21(1986), no. 2, 157–167.Google Scholar
[13] Lassak, M., Covering plane convex bodies with smaller homothetical copies. In: Intuitive Geometry. Colloq. Math. Soc. János Bolyai 48. North-Holland, Amsterdam, 1987, pp. 331–337.Google Scholar
[14] Levi, F. W., Ein geometrisches ü berdeckungsproblem. Arch. Math. 5(1954), 476–478.Google Scholar
[15] Martini, H. and Swanepoel, K. J., The geometry ofMinkowski spaces–a survey. II. Expo. Math. 22(2004), no. 2, 93–144.Google Scholar
[16] Martini, H. and Swanepoel, K. J., Antinorms and Radon curves. Aequationes Math. 72(2006), no. 1-2, 110–138.Google Scholar
[17] Martini, H., Swanepoel, K. J., and Weiss, G., The geometry of Minkowski spaces–a survey. I. Expo. Math. 19(2001), no. 2, 97–142.Google Scholar
[18] Thompson, A. C., Minkowski Geometry. Encyclopedia of Mathematics and its Applications 63, Cambridge University Press, 1996.Google Scholar
[19] Webster, R., Convexity. Oxford University Press, New York, 1994.Google Scholar