No CrossRef data available.
Article contents
A Counterexample to a Conjecture of D. B. Fuks
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In [3] D. B. Fuks defined a duality of functors in the category 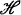 of weak homotopy types. In general this duality is more difficult to work with than the duality of functors of the category
of weak homotopy types. In general this duality is more difficult to work with than the duality of functors of the category 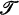 of pointed Kelley spaces [2]. It happens however that all so-called strong functors [2] F of
of pointed Kelley spaces [2]. It happens however that all so-called strong functors [2] F of 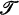 induce functors
induce functors 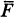 of
of 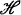 , and if we denote the duality operators of
, and if we denote the duality operators of 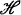 and
and 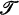 by
by 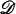 and D respectively, then there are many cases where
and D respectively, then there are many cases where 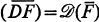 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1970
References
1.
Bott, R. and Samelson, H., On the Pontryagin product in spaces of paths, Comment. Math. Helv. 27 (1953), 320-337.Google Scholar
2.
Fuks, D. B., Eckmann- Hilton duality and the theory of functors in the category of topological spaces, Russian Math. Surveys (2) 21 (1966), 1-33.Google Scholar
3.
Fuks, D. B., Duality of functors in the category ofhomotopy types, Soviet Math. Dokl. 8 (1967), 1007-1010.Google Scholar


