Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T19:46:31.087Z Has data issue: false hasContentIssue false
  • English
  • Français

Coordinatization Theorems For Graded Algebras

Published online by Cambridge University Press:  20 November 2018

Bruce Allison  and
Oleg Smirnov
Bruce Allison
Affiliation:
Department of Mathematical and Statistical Sciences University of Alberta Edmonton, Alberta T6G 2G1, e-mail: [email protected]
Oleg Smirnov
Affiliation:
Department of Mathematics College of Charleston Charleston, South Carolina 29424-0001 USA, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we study simple associative algebras with finite 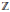$\mathbb{Z}$-gradings. This is done using a simple algebra 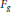${{F}_{g}}$ that has been constructed in Morita theory from a bilinear form 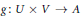$g:\,U\,\times \,V\,\to \,A$ over a simple algebra 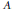$A$. We show that finite 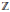$\mathbb{Z}$-gradings on 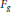${{F}_{g}}$ are in one to one correspondence with certain decompositions of the pair 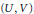$\left( U,\,V \right)$. We also show that any simple algebra 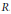$R$ with finite 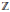$\mathbb{Z}$-grading is graded isomorphic to 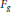${{F}_{g}}$ for some bilinear from 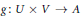$g:\,U\,\times \,V\,\to \,A$, where the grading on 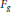${{F}_{g}}$ is determined by a decomposition of 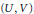$\left( U,\,V \right)$ and the coordinate algebra 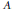$A$ is chosen as a simple ideal of the zero component 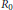${{R}_{0}}$ of 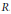$R$. In order to prove these results we first prove similar results for simple algebras with Peirce gradings.

Keywords

16W50
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 45 , Issue 4 , 01 December 2002 , pp. 451 - 465
Copyright
Copyright © Canadian Mathematical Society 2002

References

[AM] Ánh, P. N. and Márki, L., Rees matrix rings. J. Algebra 81 (1983), 340–369.Google Scholar
[A] Ara, P., Morita equivalence for rings with involutions. Algebr. Represent. Theory 2 (1999), 227–247.Google Scholar
[BSZ] Bahturin, Yu. A., Sehgal, S. K. and Zaicev, M. V., Group gradings on associative algebras. J. Algebra 241 (2001), 677–698.Google Scholar
[Be] Bergman, G. M., Radicals, tensor products and algebraicity. In: Ring Theory in Honor of S. A. Amitsur, Weizmann Science Press, Jerusalem, 1989, 150–192.Google Scholar
[BD] Boboc, C. and Dăscălescu, S. Gradings of matrix algebras by cyclic groups. Comm. Algebra 29 (2001), 5013–5021.Google Scholar
[DKvW] Dăscălescu, S., Kelarev, A. V. and van Wyk, L., Semigroup gradings of full matrix rings. Comm. Algebra 29 (2001), 5023–5031.Google Scholar
[GS] Garcia, J. L. and Simon, J. J., Morita Equivalence for idempotent rings. J. Pure Appl. Algebra 76 (1991), 39–56.Google Scholar
[J] Jacobson, N., Structure of rings. Amer.Math. Soc. Collob. Publ. 37, Providence, R.I., 1956.Google Scholar
[K] Kyono, S., Equivalence of module categories. Math. J. Okayama Univ. 28 (1986), 147–150.Google Scholar
[NvO] Năstăsescu, C. and F. Van Oystaen, Graded ring theory. North-Holland Publ. Comp. 29, 1982.Google Scholar
[S1] Smirnov, O., Simple associative algebras with finite Z-grading. J. Algebra 196 (1997), 171–184.Google Scholar
[S2] Smirnov, O., Finite Z-gradings of Lie algebras and symplectic involutions. J. Algebra 218 (1999), 246–275.Google Scholar
[ZS] Zaicev, M. V. and Sehgal, S. K., Finite gradings of simple Artinian rings. Vestnik Moskov. Univ. Ser. I Mat. Mech., (to appear).Google Scholar
[Z] Zelmanov, E. I., Lie algebras with finite Z-grading. Math. USSR-Sb. 52 (1985), 347–385.Google Scholar