Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Masson, D.
1986.
Exact Bogoliubov limits for the Bassichis–Foldy model and continued fractions.
Journal of Mathematical Physics,
Vol. 27,
Issue. 4,
p.
1093.
Masson, David R.
1987.
Schr�dinger's equation and continued fractions.
International Journal of Quantum Chemistry,
Vol. 32,
Issue. S21,
p.
699.
Masson, David R.
1988.
Nonlinear Numerical Methods and Rational Approximation.
p.
239.
Common, A K
Ebrahimi, F
and
Hafez, S T
1989.
Explicit solutions of the finite-element Schrodinger equation.
Journal of Physics A: Mathematical and General,
Vol. 22,
Issue. 16,
p.
3229.
Jacobsen, L.
and
Masson, D. R.
1990.
On the convergence of limit periodic continued fractions K(a n/1), wherea n→−1/4. Part III.
Constructive Approximation,
Vol. 6,
Issue. 4,
p.
363.
Runckel, Hans-J.
1994.
Solution formulas for linear difference equations with applications to continued fractions.
Constructive Approximation,
Vol. 10,
Issue. 2,
p.
207.
Lorentzen, Lisa
1995.
Computation of limit periodic continued fractions. A survey.
Numerical Algorithms,
Vol. 10,
Issue. 1,
p.
69.
Lorentzen, Lisa
1997.
Asymptotic Behavior of Solutions of Three-Term Poincaré Difference Equations.
Rocky Mountain Journal of Mathematics,
Vol. 27,
Issue. 1,
Rahman, Mizan
2001.
Special Functions 2000: Current Perspective and Future Directions.
p.
255.
Ismail, Mourad E.H.
and
Muldoon, Martin E.
2012.
A tribute to David Masson.
Journal of Approximation Theory,
Vol. 164,
Issue. 2,
p.
211.
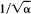 for an even larger class of C-fractions is proved for the case
for an even larger class of C-fractions is proved for the case 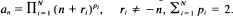 .
.