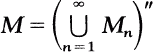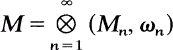Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
1981.
Von Neumann Algebras.
Vol. 27,
Issue. ,
p.
387.
Hawkins, Jane
1982.
Non-itpfidiffeomorphisms.
Israel Journal of Mathematics,
Vol. 42,
Issue. 1-2,
p.
117.
Giordano, T
and
Skandalis, G
1985.
Krieger factors isomorphic to their tensor square and pure point spectrum flows.
Journal of Functional Analysis,
Vol. 64,
Issue. 2,
p.
209.
Connes, A.
and
Woods, E. J.
1985.
Approximately transitive flows and ITPFI factors.
Ergodic Theory and Dynamical Systems,
Vol. 5,
Issue. 2,
p.
203.
Vershik, A. M.
and
Fedorov, A. L.
1987.
Trajectory theory.
Journal of Soviet Mathematics,
Vol. 38,
Issue. 2,
p.
1799.
Kawahigashi, Y.
Sutherland, C. E.
and
Takesaki, M.
1992.
The structure of the automorphism group of an injective factor and the cocycle conjugacy of discrete abelian group actions.
Acta Mathematica,
Vol. 169,
Issue. 0,
p.
105.
Falcone, Tony
and
Takesaki, Masamichi
2001.
The Non-commutative Flow of Weights on a Von Neumann Algebra.
Journal of Functional Analysis,
Vol. 182,
Issue. 1,
p.
170.
Sasyk, Román
and
Törnquist, Asger
2010.
Turbulence and Araki–Woods factors.
Journal of Functional Analysis,
Vol. 259,
Issue. 9,
p.
2238.