Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-01-12T23:40:58.776Z Has data issue: false hasContentIssue false
  • English
  • Français

Constructing an Automorphism From an Anti-Automorphism

Published online by Cambridge University Press:  20 November 2018

Christine Ayoub
Christine Ayoub*
Affiliation:
Pennsylvania State University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the following problem: Let G be a group with distinct automorphisms β and σ and an anti-automorphism α such that

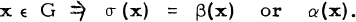
What can be said about G?

If σ = α, σ is both an automorphism and an anti-automorphism so that G is abelian. Hence we assume that σ ≠ α. In this case, we show that G is non-abelian, but has an abelian subgroup of index 2. Conversely, for such a group G there always exist distinct automorphisms β and σ and an anti-automorphism α such that (1) holds.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 11 , Issue 3 , August 1968 , pp. 367 - 370
Copyright
Copyright © Canadian Mathematical Society 1968