Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Saksman, Eero
and
Tylli, Hans-Olav
1993.
Compact and inessential perturbations of operators with closed range.
Integral Equations and Operator Theory,
Vol. 17,
Issue. 3,
p.
404.
Mbekhta, Mostafa
2002.
Formules de distance au spectre généralisé et au spectre semi-Fredholm.
Journal of Functional Analysis,
Vol. 194,
Issue. 2,
p.
231.
Boasso, Enrico
2008.
On the Moore–Penrose inverse, EP Banach space operators, and EP Banach algebra elements.
Journal of Mathematical Analysis and Applications,
Vol. 339,
Issue. 2,
p.
1003.
Mbekhta, Mostafa
2009.
A HUA TYPE THEOREM AND LINEAR PRESERVER PROBLEMS.
Mathematical Proceedings of the Royal Irish Academy,
Vol. 109,
Issue. 2,
p.
109.
Boasso, Enrico
2011.
Factorizations of EP Banach space operators and EP Banach algebra elements.
Journal of Mathematical Analysis and Applications,
Vol. 379,
Issue. 1,
p.
245.
Benítez, Julio
Boasso, Enrico
and
Xu, Sanzhang
2020.
On the continuity and differentiability of the (dual) core inverse in C*-algebras.
Linear and Multilinear Algebra,
Vol. 68,
Issue. 4,
p.
686.
Cassier, Gilles
and
Perrin, Thomas
2021.
Aluthge Operator Field and Its Numerical Range and Spectral Properties.
Integral Equations and Operator Theory,
Vol. 93,
Issue. 4,
Mbekhta, Mostafa
2023.
The local reduced minimum modulus on a Hilbert space.
Acta Scientiarum Mathematicarum,
Vol. 89,
Issue. 1-2,
p.
269.
Baklouti, H.
Difaoui, K.
and
Mabrouk, M.
2024.
On the A-spectrum for A-bounded operators on von-Neumann algebras.
Advances in Operator Theory,
Vol. 9,
Issue. 3,
Bourhim, Abdellatif
and
Mbekhta, Mostafa
2025.
The M-reduced minimum modulus of operators.
Journal of Mathematical Analysis and Applications,
Vol. 546,
Issue. 1,
p.
129202.
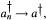 où a† désigne l'inverse de Moore-Penrose de a.
où a† désigne l'inverse de Moore-Penrose de a.

