Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-20T18:26:17.982Z Has data issue: false hasContentIssue false
  • English
  • Français

Conjugate Radius and Sphere Theorem

Published online by Cambridge University Press:  20 November 2018

Seong-Hun Paeng  and
Jong-Gug Yun
Seong-Hun Paeng
Affiliation:
Korea Institute for Advanced Study (KIAS) 207-43 Cheongryangri-dong Dongdaemun-gu Seoul 130-012 Korea, email: [email protected]
Jong-Gug Yun
Affiliation:
Department of Mathematics Seoul National University Seoul 151-742 Korea, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Bessa [Be] proved that for given $n$ and 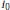${{i}_{0}}$, there exists an 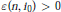$\varepsilon (\text{n,}\,{{i}_{0}})\,>\,0$ depending on $n$, 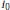${{i}_{0}}$ such that if 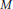$M$ admits a metric $g$ satisfying 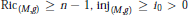$\text{Ri}{{\text{c}}_{(M,g)}}\ge n-1,\text{in}{{\text{j}}_{(M,g)}}\ge {{i}_{0}}\,>\,0$ and 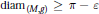$\text{dia}{{\text{m}}_{(M,g)}}\,\ge \,\pi \,-\,\varepsilon $, then 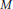$M$ is diffeomorphic to the standard sphere. In this note, we improve this result by replacing a lower bound on the injectivity radius with a lower bound of the conjugate radius.

Keywords

53C2053C21Ricci curvatureconjugate radius
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 42 , Issue 2 , 01 June 1999 , pp. 214 - 220
Copyright
Copyright © Canadian Mathematical Society 1999

References

[AC] Anderson, M. T. and J. Cheeger, Cα-compactness for manifolds with Ricci curvature and injectivity radius bounded below. J. Differential Geom. 35 (1992), 265–281.Google Scholar
[Be] Bessa, G. P., Differentiable sphere theorems for Ricci curvature. Math. Z. 214 (1993), 245–259.Google Scholar
[BC] Bishop, R. and Crittenden, B., Geometry of manifolds. Academic Press, New York, 1964.Google Scholar
[BK] Buser, P. and Karcher, H., Gromov's almost flat manifolds. Astérisque 81 (1981).Google Scholar
[Br] Brocks, R., Convexité et courbure de Ricci.C. R. Acad. Sci. Paris Sér. I 319 (1994), 73–75.Google Scholar
[Ca] Cai, M., A splitting theoremfor manifolds of almost nonnegative Ricci curvature. Ann. Global Anal. Geom. 11 (1993), 373–385.Google Scholar
[CCo1] Cheeger, J. and Colding, T. H., Lower bounds on Ricci curvature and the almost rigidity of warped products. Ann. ofMath. 144 (1996), 189–237.Google Scholar
[CCo2] Cheeger, J. and Colding, T. H., On the structure of spaces with Ricci curvature bounded below. Preprint.Google Scholar
[CE] Cheeger, J. and Ebin, D. G., Comparison theorems in Riemannian geometry. Amsterdam, 1975.Google Scholar
[CH] Calabi, E. and Hartman, P., On the smoothness of isometries. Duke Math. J. 37 (1970), 741–750.Google Scholar
[Cr] Croke, C., An eigenvalue pinching theorem. Invent.Math. 68 (1982), 253–256.Google Scholar
[DSW] Dai, X., Shen, Z. and Wei, G., Negative Ricci curvature and isometry group.DukeMath. J. 76 (1994), 59–73.Google Scholar
[DW] Dai, X. and Wei, G., A comparison estimate of Toponogov type for Ricci curvature.Math. Ann. 303 (1995), 297–306.Google Scholar
[GHL] Gallot, S., Hulin, D. and Lafontaine, J., Riemannian geometry. Springer-Verlag, 1987.Google Scholar
[O] Otsu, Y., On manifolds of small excess. Amer. J. Math. 115 (1993), 1229–1280.Google Scholar
[P1] Paeng, S.-H., Topological entropy for geodesic flows under a Ricci curvature condition. Proc. Amer. Math. Soc. 125 (1997), 1873–1879.Google Scholar
[P2] Paeng, S.-H., A generalization of Gromov's almost flat manifolds and topological entropy for geodesic flow. Preprint.Google Scholar
[Wei] Wei, G., Ricci curvature and Betti number. J. Geom. Anal., to appear.Google Scholar