Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-14T15:17:14.365Z Has data issue: false hasContentIssue false
  • English
  • Français

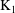The Coniveau Filtration on $\text{K}_{1}$ for Some Severi–Brauer Varieties

Part of: $K$-theory in geometry Cycles and subschemes

Published online by Cambridge University Press:  24 October 2018

Eoin Mackall
Eoin Mackall*
Affiliation:
Mathematical & Statistical Sciences, University of Alberta, Edmonton, AB Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We produce an isomorphism 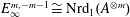$E_{\infty }^{m,-m-1}\cong \text{Nrd}_{1}(A^{\otimes m})$ between terms of the 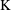$\text{K}$-theory coniveau spectral sequence of a Severi–Brauer variety 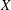$X$ associated with a central simple algebra 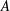$A$ and a reduced norm group, assuming 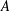$A$ has equal index and exponent over all finite extensions of its center and that 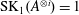$\text{SK}_{1}(A^{\otimes i})=1$ for all 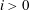$i>0$.

Keywords

Severi–Brauer varietyconiveau spectral sequence

MSC classification

Primary: 19E08: $K$-theory of schemes
Secondary: 14C35: Applications of methods of algebraic $K$-theory
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 3 , September 2019 , pp. 565 - 576
Copyright
© Canadian Mathematical Society 2018 

References

Artin, M., Brauer-Severi varieties, Brauer groups in ring theory and algebraic geometry . (Wilrijk, 1981), Lecture Notes in Mathematics, 917, Springer, Berlin–New York, 1982, pp. 194–210.Google Scholar
Chernousov, V. and Merkurjev, A., Connectedness of classes of fields and zero-cycles on projective homogeneous varieties . Compos. Math. 142(2006), no. 6, 1522–1548. https://doi.org/10.1112/S0010437X06002363.Google Scholar
de Jong, A. J., The period-index problem for the Brauer group of an algebraic surface . Duke Math. J. 123(2004), no. 1, 71–94. https://doi.org/10.1215/S0012-7094-04-12313-9.Google Scholar
Gille, P. and Szamuely, T., Central simple algebras and Galois cohomology . Cambridge Studies in Advanced Mathematics, 101, Cambridge University Press, Cambridge, 2006. https://doi.org/10.1017/CBO9780511607219.Google Scholar
Karpenko, N. A., Codimension 2 cycles on Severi–Brauer varieties . K-Theory 13(1998), no. 4, 305–330. https://doi.org/10.1023/A:1007705720373.Google Scholar
Karpenko, N. A., Cohomology of relative cellular spaces and of isotropic flag varieties . Algebra i Analiz 12(2000), no. 1, 3–69.Google Scholar
Karpenko, N. A., Chow groups of some generically twisted flag varieties . Ann. K-Theory 2(2017), no. 2, 341–356. https://doi.org/10.2140/akt.2017.2.341.Google Scholar
Merkurjev, A. S., Certain K-cohomology groups of Severi–Brauer varieties . In: K-theory and algebraic geometry: connections with quadratic forms and division algebras (Santa Barbara, CA, 1992) , Proc. Sympos. Pure Math., 58, American Mathematical Society, Providence, RI, 1995, pp. 319–331.Google Scholar
Merkurjev, A. S. and Suslin, A. A., K-cohomology of Severi–Brauer varieties and the norm residue homomorphism . Izv. Akad. Nauk SSSR Ser. Mat. 46(1982), no. 5, 1011–1046, 1135–1136.Google Scholar
Perlis, S., Scalar extensions of algebras with exponent equal to index . Bull. Amer. Math. Soc. 47(1941), 670–676. https://doi.org/10.1090/S0002-9904-1941-07536-1.Google Scholar
Peyre, E., Products of Severi–Brauer varieties and Galois cohomology . In: K-theory and algebraic geometry: connections with quadratic forms and division algebras (Santa Barbara, CA, 1992) , Proc. Sympos. Pure Math., 58, American Mathematical Society, Providence, RI, 1995, pp. 369–401.Google Scholar
Quillen, D., Higher algebraic K-theory. I . In: Algebraic K-theory, I: Higher K-theories (Proc. Conf., Battelle Memorial Inst., Seattle, Wash., 1972) , Lecture Notes in Mathematics, 341, Springer, Berlin, 1973, pp. 85–147.Google Scholar