Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T16:02:29.470Z Has data issue: false hasContentIssue false
  • English
  • Français

A Congruence for a Class of Arithmetic Functions

Published online by Cambridge University Press:  20 November 2018

M.V. Subbarao
M.V. Subbarao*
Affiliation:
University of Alberta, Edmonton
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

There is considerable literature concerning the century old result that for arbitrary positive integers a and m,

1.1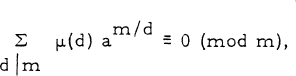

where μ(m) is the usual Mobius function. For earlier work on this we refer to L.E. Dickson [4, pp. 84–86] and L. Carlitz [1,2]. Another reference not noted by the above authors is R. Vaidyanathaswamy [6], who noted that the left member of (1.1) represents the number of special fixed points of the m th power of a rational transformation of the n th degree.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 9 , Issue 5 , December 1966 , pp. 571 - 574
Copyright
Copyright © Canadian Mathematical Society 1966

References

1. Carlitz, L., An arithmetic function. Bull. Amer. Math. Soc. 43, (1937), pages 271-276.Google Scholar
2. Carlitz, L., Note on an arithmetic function. Amer. Math. Monthly, 59, (1952), pages 386-387.Google Scholar
3. Cashwell, E.D. and Everett, C.J., The ring of number theoretic functions. Pacific J. of Math. 9, (1959), pages 975-985.Google Scholar
4. Dickson, L.E., History of the Theory of Numbers. Vol. I.Google Scholar
5. McCarthy, P.J., On an arithmetic function. Monatsh Math. 63, (1959), pages 228-230.Google Scholar
6. Vaidyanathaswamy, R., Collected papers. Madras University.Google Scholar