Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T06:58:11.331Z Has data issue: false hasContentIssue false
  • English
  • Français

Congruence Class Sizes in Finite Sectionally Complemented Lattices

Published online by Cambridge University Press:  20 November 2018

G. Grätzer  and
E. T. Schmidt
G. Grätzer
Affiliation:
Department of Mathematics University of Manitoba Winnipeg, MB R3T 2N2, email: [email protected], http://www.math.umanitoba.ca/homepages/gratzer/
E. T. Schmidt
Affiliation:
Mathematical Institute of the Budapest University of Technology and Economics Műegyetem rkp. 3 H-1521 Budapest Hungary email:[email protected]://www.math.bme.hu/∼schmidt/
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The congruences of a finite sectionally complemented lattice 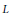$L$ are not necessarily uniform (any two congruence classes of a congruence are of the same size). To measure how far a congruence 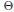$\Theta $ of 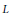$L$ is from being uniform, we introduce Spec 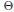$\Theta $, the spectrum of 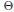$\Theta $, the family of cardinalities of the congruence classes of 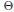$\Theta $. A typical result of this paper characterizes the spectrum 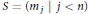$S=({{m}_{j}}|j<n)$ of a nontrivial congruence 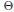$\Theta $ with the following two properties:

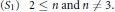$$({{S}_{1}})\,\,\,\,2\le n\,\,\text{and }n\ne 3.\,\,\,\,$$
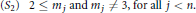$$({{S}_{2}})\,\,\,2\le {{m}_{j}}\,\,\text{and}\,\,{{m}_{j}}\ne 3,\,\,\,\text{for}\,\text{all}\,j<n.$$

Keywords

06B1006B15congruence latticecongruence-preserving extension
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 47 , Issue 2 , 01 June 2004 , pp. 191 - 205
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Grätzer, G., General Lattice Theory, Second edition: New appendices by the author with B. A. Davey, R. Freese, B. Ganter, M. Greferath, P. Jipsen, H. A. Priestley, H. Rose, E. T. Schmidt, S. E. Schmidt, F. Wehrung, and R.Wille. Birkhäuser Verlag, Basel, 1998.Google Scholar
[2] Grätzer, G. and Schmidt, E. T., On congruence lattices of lattices. Acta Math. Acad. Sci. Hungar. 13 (1962), 179–185.Google Scholar
[3] Grätzer, G. and Schmidt, E. T., Congruence-preserving extensions of finite lattices into sectionally complemented lattices. Proc. Amer. Math. Soc. 127 (1999), 1903–1915.Google Scholar
[4] Grätzer, G. and Schmidt, E. T., Finite lattices with isoform congruences. Tatra Mt. Math. Publ. 27 (2003), 1–14.Google Scholar