No CrossRef data available.
Article contents
Condition 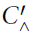 $C_{\hat{\ }}^{'}$, of Operator Spaces
$C_{\hat{\ }}^{'}$, of Operator Spaces
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In this paper, we study condition 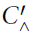 $C_{\hat{\ }}^{'}$, which is a projective tensor product analogue of condition
$C_{\hat{\ }}^{'}$, which is a projective tensor product analogue of condition  $C'$. We show that the finite-dimensional
$C'$. We show that the finite-dimensional 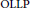 $\text{OLLP}$ operator spaces have condition
$\text{OLLP}$ operator spaces have condition 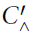 $C_{\hat{\ }}^{'}$, and
$C_{\hat{\ }}^{'}$, and 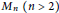 ${{M}_{n}}\left( n\,>\,2 \right)$ does not have that property.
${{M}_{n}}\left( n\,>\,2 \right)$ does not have that property.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2017
References
[1]
Archbold, R. J. and Batty, C. J., C*-tensor norms and slice maps.
J. London Math. Soc.
22(1980), no. 1, 127–138. http://dx.doi.Org/10.1112/jlms/s2-22.1.127
Google Scholar
[2]
Blecher, D. P., Tensor products of operator spaces. II.
Canad. J. Math.
44(1992), no. 1, 75–90. http://dx.doi.Org/10.4153/CJM-1992-004-5
Google Scholar
[3]
Blecher, D. P. and Paulsen, V. I., Tensor products of operator spaces.
J. Funct. Anal.
99(1991), 262–292. http://dx.doi.Org/10.101 6/0022-1236(91 )90042-4
Google Scholar
[4]
Dong, Z., The OLLP and 7-local reflexivity of operator spaces.
Illinois J. Math.
51(2006), 1103–1122.Google Scholar
[5]
Effros, E. G. and Haagerup, U., Lifting problems and local reflexivity for C*-algebras.
Duke Math. J.
52(1985), 103–128. http://dx.doi.Org/10.1215/S0012-7094-85-05207-X
Google Scholar
[6]
Effros, E. G., Junge, M., and Ruan, Z.-J., Integral mapping and the principle of local reflexive for non-commutative L1 spaces.
Ann. of Math.
151(2000), no. 1, 59-92. http://dx.doi.Org/10.2307/121112
Google Scholar
[7]
Effros, E. G. and Ruan, Z.-J., On approximation properties for operator spaces.
Internat. J. Math.
1(1990), 163–181. http://dx.doi.Org/10.1142/S01291 67X90000113
Google Scholar
[8]
Effros, E. G. and Ruan, Z.-J., Mapping spaces and liftings for operator spaces.
Proc. London Math. Soc.
69(1994), 171–197. http://dx.doi.Org/10.1112/plms/s3-69.1.171
Google Scholar
[9]
Effros, E. G. and Ruan, Z.-J., The Grothedieck-Pietsch and Dvoretzky-Rogers theory for operator spaces.
J. Funct. Anal.
122(1994), 428–450. http://dx.doi.Org/10.1006/jfan.1994.1075
Google Scholar
[10]
Effros, E. G. and Ruan, Z.-J., On the analogues of integral mappings and local reflexivity for operator spaces.
Indiana Univ. Math. J.
46(1997), 1289–1310. http://dx.doi.Org/10.1512/iumj.1997.46.1429
Google Scholar
[11]
Effros, E. G. and Ruan, Z.-J., Operator spaces. London Mathematical Society Monographs. New Series, 23, The Clarendon Press, Oxford University Press, New York, 2000.Google Scholar
[12]
Han, K. H., An operator space approach to condition C.
J. Math. Anal. Appl.
336(2007), 569–576. http://dx.doi.Org/10.1016/j.jmaa.2007.02.074
Google Scholar
[13]
Kirchberg, E., The Fubini theory for exact C*-algebras.
J. Operator Theory
10(1983), 3–8.Google Scholar
[14]
Kirchberg, E., On non-semisplit extensions, tensor products and exactness of group C*-algebras.
Invent. Math.
112(1993), 449–489. http://dx.doi.Org/10.1007/BF01232444
Google Scholar
[15]
Kirchberg, E., On subalgebras of the CAR-algebra.
J. Funct. Anal.
129(1995), 35–63. http://dx.doi.Org/10.1006/jfan.1 995.1041
Google Scholar
[16]
Ozawa, N., On the lifting property for universal C*-algebras of operator spaces.
J. Operator Theory
46(2001), no. 3, 579–591.Google Scholar
[17]
Pisier, G., Exact operator spaces. Recent advances in operator algebras (Orléans, 1992).
Astérisque
233(1995), 159–186.Google Scholar
[18]
Pisier, G., Introduction to operator space theory. London Mathematical Society Lecture Note Series, 294, Cambridge University Press, Cambridge, 2003. http://dx.doi.Org/10.1017/CBO9781107360235
Google Scholar
[19]
Ruan, Z.-J., Subspaces of C*-algebras.
J. Funct. Anal.
76(1988), 217–230. http://dx.doi.Org/!0.1016/0022-1236(88)90057-2
Google Scholar


