Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T01:09:37.094Z Has data issue: false hasContentIssue false
  • English
  • Français

Condensed Domains

Published online by Cambridge University Press:  20 November 2018

D. D. Anderson  and
Tiberiu Dumitrescu
D. D. Anderson
Affiliation:
Department of Mathematics, The University of Iowa, Iowa City, Iowa 52242-1419, U.S.A.
Tiberiu Dumitrescu
Affiliation:
Facultatea de Matematică, Universitatea Bucureşti, 14 Academiei Str., Bucharest 70109, Romania
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An integral domain 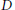$D$ with identity is condensed (resp., strongly condensed) if for each pair of ideals 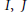$I,\,J$ of 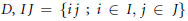$D,\,IJ\,=\,\{ij\,;\,i\,\in I,j\in J\,\}$ (resp., 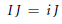$IJ=iJ$ for some 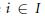$i\,\in \,I$ or 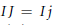$IJ\,=Ij$ for some 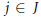$j\,\in \,J$). We show that for a Noetherian domain 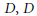$D,\,D$ is condensed if and only if 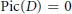$\text{Pic}\left( D \right)\,=0$ and 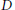$D$ is locally condensed, while a local domain is strongly condensed if and only if it has the two-generator property. An integrally closed domain 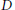$D$ is strongly condensed if and only if 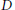$D$ is a Bézout generalized Dedekind domain with at most one maximal ideal of height greater than one. We give a number of equivalencies for a local domain with finite integral closure to be strongly condensed. Finally, we show that for a field extension 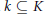$k\,\subseteq K$, the domain 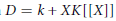$D=\,k+XK[[X]]$ is condensed if and only if 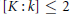$[K:k]\,\le \,2$ or 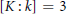$[K:k]\,=\,3$ and each degree-two polynomial in 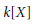$k[X]$ splits over 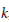$k$, while 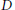$D$ is strongly condensed if and only if 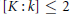$[K:k]\,\le \,2$.

Keywords

13A1513B22
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 46 , Issue 1 , 01 March 2003 , pp. 3 - 13
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Anderson, D. D. and Mahaney, L. A., On primary factorizations. J. Pure Appl. Algebra 54 (1988), 141–154.Google Scholar
[2] Anderson, D. D. and Zafrullah, M., Independent locally-finite intersections of localizations. Houston J. Math. 15 (1999), 433–452.Google Scholar
[3] Anderson, D. F., Arnold, J. T. and Dobbs, D. E., Integrally closed condensed domains are Bézout. Canad. Math. Bull. 28 (1985), 98–102.Google Scholar
[4] Anderson, D. F. and Dobbs, D. E., On the product of ideals. Canad. Math. Bull. 26 (1983), 106–114.Google Scholar
[5] Facchini, A., Generalized Dedekind domains and their injective modules. J. Pure Appl. Algebra 94 (1994), 159–173.Google Scholar
[6] Fontana, M., Huckaba, J. and Papick, I., Prüfer Domains. Marcel Dekker, New York, 1997.Google Scholar
[7] Gabelli, S. and Popescu, N., Invertible and divisorial ideals of a generalized Dedekind domain. J. Pure Appl. Algebra 135 (1999), 237–251.Google Scholar
[8] Gilmer, R., Multiplicative Ideal Theory. Marcel Dekker, New York, 1972.Google Scholar
[9] Gottlieb, C., On condensed Noetherian integral domains whose integral closures are discrete valuation rings. Canad. Math. Bull. 32 (1989), 166–168.Google Scholar
[10] Greither, C., On the two-generator problem for ideals of a one-dimensional ring. J. Pure Appl. Algebra 24 (1982), 265–276.Google Scholar
[11] Handelman, D., Propinquity of one-dimensional Gorenstein rings. J. Pure Appl. Algebra 24 (1982), 145–150.Google Scholar
[12] Jacobson, N., Basic Algebra I. Freeman, San Francisco, 1974.Google Scholar
[13] Nagata, M., Local Rings. Interscience, New York and London, 1962.Google Scholar
[14] Olberding, B., Factorization into prime and invertible ideals. J. London Math. Soc. 62 (2000), 336–344.Google Scholar
[15] Rush, D. E., Rings with two-generated ideals. J. Pure Appl. Algebra 73 (1991), 257–275.Google Scholar
[16] Sally, J. and Vasconcelos, W., Stable rings and a problem of Bass. Bull. Amer.Math. Soc. 79 (1973), 574–576.Google Scholar
[17] Wiegand, R., Cancellation over commutative rings of dimension one and two. J. Algebra 88(1984), 438–459.Google Scholar