Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-01T23:39:06.177Z Has data issue: false hasContentIssue false
  • English
  • Français

A Compact Imbedding Theorem for Functions without Compact Support

Published online by Cambridge University Press:  20 November 2018

R. A. Adams  and
John Fournier
R. A. Adams
Affiliation:
University of British Columbia, Vancouver, British Columbia
John Fournier
Affiliation:
University of British Columbia, Vancouver, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The extension of the Rellich-Kondrachov theorem on the complete continuity of Sobolev space imbeddings of the sort

1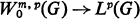

to unbounded domains G has recently been under study [1–5] and this study has yielded [4] a condition on G which is necessary and sufficient for the compactness of (1). Similar compactness theorems for the imbeddings

2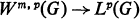

are well known for bounded domains G with suitably regular boundaries, and the question naturally arises whether any extensions to unbounded domains can be made in this case.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 14 , Issue 3 , September 1971 , pp. 305 - 309
Copyright
Copyright © Canadian Mathematical Society 1971

References

1. Adams, R. A., Compact Sobolev imbeddings for unbounded domains, Pacific J. Math. 32 (1970), 1-7.Google Scholar
2. Adams, R. A., The Rellich Kondrachov theorem for unbounded domains, Arch. Rational Mech. Anal. 29 (1968), 390-394.Google Scholar
3. Adams, R. A., Compact imbedding theorems for quasibounded domains, Trans. Amer. Math. Soc. 148 (1970), 445-459.Google Scholar
4. Adams, R. A., Capacity and compact imbeddings, J. Math. Mech. 19 (1970), 923-929.Google Scholar
5. Clark, C. W., An embedding theorem for function spaces, Pacific J. Math. 19 (1966), 243-251.Google Scholar