Published online by Cambridge University Press: 20 November 2018
Dealing with the cardinal invariants  $\mathfrak{p}$ and
$\mathfrak{p}$ and  $\mathfrak{t}$ of the continuum, we prove that
$\mathfrak{t}$ of the continuum, we prove that
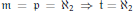 $\mathfrak{m}\,=\,\mathfrak{p}\,=\,{{\aleph }_{2}}\,\Rightarrow \,\mathfrak{t}\,=\,{{\aleph }_{2}}$
. In other words, if
$\mathfrak{m}\,=\,\mathfrak{p}\,=\,{{\aleph }_{2}}\,\Rightarrow \,\mathfrak{t}\,=\,{{\aleph }_{2}}$
. In other words, if
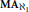 $\text{M}{{\text{A}}_{{{\aleph }_{1}}}}$
(or a weak version of this) holds, then (of course
$\text{M}{{\text{A}}_{{{\aleph }_{1}}}}$
(or a weak version of this) holds, then (of course
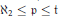 ${{\aleph }_{2}}\,\le \,\mathfrak{p}\,\le \,\mathfrak{t}$
and)
${{\aleph }_{2}}\,\le \,\mathfrak{p}\,\le \,\mathfrak{t}$
and)
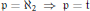 $\mathfrak{p}\,=\,\,{{\aleph }_{2}}\,\Rightarrow \,\mathfrak{p}\,=\,\mathfrak{t}$
. The proof is based on a criterion for
$\mathfrak{p}\,=\,\,{{\aleph }_{2}}\,\Rightarrow \,\mathfrak{p}\,=\,\mathfrak{t}$
. The proof is based on a criterion for 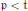 $\mathfrak{p}\,<\,\mathfrak{t}$.
$\mathfrak{p}\,<\,\mathfrak{t}$.