Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-30T17:01:48.154Z Has data issue: false hasContentIssue false
  • English
  • Français

A Combinatorial Proof of a Conjecture of Goldberg and Moon

Published online by Cambridge University Press:  20 November 2018

Brian Alspach
Brian Alspach*
Affiliation:
Simon Fraser University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Tn denote a tournament of order n, let G(Tn) denote the automorphism group of Tn, let |G| denote the order of the group G, and let g(n) denote the maximum of |G(Tn)| taken over all tournaments Tn of order n. Goldberg and Moon conjectured [2] that 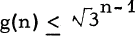for all n≥1 with equality holding if and only if n is a power of 3. In an addendum to [2] it was pointed out that their conjecture is equivalent to the conjecture that if G is any odd order subgroup of Sn, the symmetric group of degree n, then 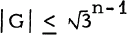with equality possible if and only if n is a power of 3. The latter conjecture was proved in [1] by John D. Dixon who made use of the Feit-Thompson theorem in his proof. In this paper we avoid use of the Feit-Thompson result and give a combinatorial proof of the Goldberg-Moon conjecture.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 11 , Issue 5 , December 1968 , pp. 655 - 661
Copyright
Copyright © Canadian Mathematical Society 1968

References

1. Dixon, John D., The maximum order of the group of a tournament. Canad. Math. Bull. 10 (1967) 503-505.Google Scholar
2. Goldberg, M. and Moon, J.W., On the maximum order of the group of a tournament. Canad. Math. Bull. 9 (1966) 563-569.Google Scholar
3. Wielandt, H., Finite permutation groups. (Transi. R. Bercov). (Academic Press, New York, 1964).Google Scholar