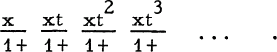Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Giles, J. R.
and
Wallis, Jennifer Seberry
1976.
George Szekeres.
Journal of the Australian Mathematical Society,
Vol. 21,
Issue. 4,
p.
385.
Takács, Lajos
1986.
Some asymptotic formulas for lattice paths.
Journal of Statistical Planning and Inference,
Vol. 14,
Issue. 1,
p.
123.
Odlyzko, Andrew M.
and
Wilf, Herbert S.
1988.
The Editor's Corner: n Coins in a Fountain.
The American Mathematical Monthly,
Vol. 95,
Issue. 9,
p.
840.
Takács, Lajos
1991.
A bernoulli excursion and its various applications.
Advances in Applied Probability,
Vol. 23,
Issue. 3,
p.
557.
Takács, Lajos
1991.
A bernoulli excursion and its various applications.
Advances in Applied Probability,
Vol. 23,
Issue. 3,
p.
557.
Takács, L.
1992.
Probability Theory and Applications.
p.
1.
Chung, Fan
Graham, Ron
Morrison, John
and
Odlyzko, Andrew
1995.
Pebbling a Chessboard.
The American Mathematical Monthly,
Vol. 102,
Issue. 2,
p.
113.
OPPENHEIM, A. C.
BRAK, R.
and
OWCZAREK, A. L.
2002.
ANISOTROPIC STEP, SURFACE CONTACT, AND AREA WEIGHTED DIRECTED WALKS ON THE TRIANGULAR LATTICE.
International Journal of Modern Physics B,
Vol. 16,
Issue. 09,
p.
1269.
Battagliola, Michele
Murru, Nadir
and
Santilli, Giordano
2023.
Combinatorial properties of multidimensional continued fractions.
Discrete Mathematics,
Vol. 346,
Issue. 12,
p.
113649.