No CrossRef data available.
Article contents
A Cohomological Property of π-invariant Elements
Published online by Cambridge University Press: 20 November 2018
Abstract.
Let  $A$ be a Banach algebra and let
$A$ be a Banach algebra and let 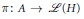 $\pi :\,A\,\to \,\mathcal{L}\left( H \right)$ be a continuous representation of
$\pi :\,A\,\to \,\mathcal{L}\left( H \right)$ be a continuous representation of  $A$ on a separable Hilbert space
$A$ on a separable Hilbert space  $H$ with dim
$H$ with dim 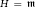 $H\,=\,\text{m}$. Let
$H\,=\,\text{m}$. Let 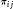 ${{\pi }_{ij}}$ be the coordinate functions of
${{\pi }_{ij}}$ be the coordinate functions of  $\pi $ with respect to an orthonormal basis and suppose that for each
$\pi $ with respect to an orthonormal basis and suppose that for each 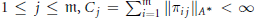 $1\,\le \,j\,\le \,\text{m,}\,{{C}_{j}}\,=\,\sum\nolimits_{i=1}^{\text{m}}{\left\| {{\pi }_{ij}} \right\|}{{A}^{*}}\,<\,\infty $ and
$1\,\le \,j\,\le \,\text{m,}\,{{C}_{j}}\,=\,\sum\nolimits_{i=1}^{\text{m}}{\left\| {{\pi }_{ij}} \right\|}{{A}^{*}}\,<\,\infty $ and 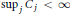 ${{\sup }_{j}}\,{{C}_{j}}\,<\,\infty $. Under these conditions, we call an element
${{\sup }_{j}}\,{{C}_{j}}\,<\,\infty $. Under these conditions, we call an element 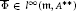 $\overline{\Phi }\,\in \,{{\iota }^{\infty }}\,\left( \mathfrak{m},\,{{A}^{**}} \right)$ left
$\overline{\Phi }\,\in \,{{\iota }^{\infty }}\,\left( \mathfrak{m},\,{{A}^{**}} \right)$ left  $\pi $-invariant if
$\pi $-invariant if 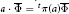 $a\,\cdot \overline{\Phi }\,={{\,}^{^{t}\pi }}\left( a \right)\overline{\Phi }$ for all
$a\,\cdot \overline{\Phi }\,={{\,}^{^{t}\pi }}\left( a \right)\overline{\Phi }$ for all 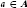 $a\in A$ In this paper we prove a link between the existence of left
$a\in A$ In this paper we prove a link between the existence of left  $\pi $-invariant elements and the vanishing of certain Hochschild cohomology groups of
$\pi $-invariant elements and the vanishing of certain Hochschild cohomology groups of  $A$. Our results extend an earlier result by Lau on
$A$. Our results extend an earlier result by Lau on  $F$-algebras and recent results of Kaniuth, Lau, Pym, and and the second author in the special case where
$F$-algebras and recent results of Kaniuth, Lau, Pym, and and the second author in the special case where 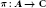 $\pi :\,A\,\to \text{C}$ is a non-zero character on
$\pi :\,A\,\to \text{C}$ is a non-zero character on  $A$.
$A$.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2013


