Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T17:42:15.509Z Has data issue: false hasContentIssue false
  • English
  • Français

Cohomological Dimension and Schreier's Formula in Galois Cohomology

Published online by Cambridge University Press:  20 November 2018

John Labute ,
Nicole Lemire ,
Ján Mináč  and
John Swallow
John Labute
Affiliation:
Department of Mathematics and Statistics, McGill University, 805 Sherbrooke StreetWest, Montreal, QC, H3A 2K6 e-mail: [email protected]
Nicole Lemire
Affiliation:
Department of Mathematics, Middlesex College, University of Western Ontario, London, ON, N6A 5B7 e-mail: [email protected]@uwo.ca
Ján Mináč
Affiliation:
Department of Mathematics, Middlesex College, University of Western Ontario, London, ON, N6A 5B7 e-mail: [email protected]@uwo.ca
John Swallow
Affiliation:
Department of Mathematics, Davidson College, Davidson, NC 28035-7046, U.S.A. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 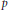$p$ be a prime and $F$ a field containing a primitive 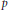$p$-th root of unity. Then for 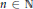$n\,\in \,\mathbb{N}$, the cohomological dimension of the maximal pro-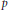$p$-quotient 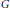$G$ of the absolute Galois group of $F$ is at most $n$ if and only if the corestriction maps 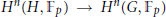${{H}^{n}}\left( H,\ {{\mathbb{F}}_{p}} \right)\,\to \,{{H}^{n}}\left( G,\ {{\mathbb{F}}_{p}} \right)$ are surjective for all open subgroups 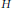$H$ of index 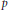$p$. Using this result, we generalize Schreier's formula for 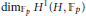${{\dim}_{{{\mathbb{F}}_{p}}}}\,{{H}^{1}}\,\left( H,\ {{\mathbb{F}}_{p}} \right)$ to 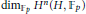${{\dim}_{{{\mathbb{F}}_{p}}}}{{H}^{n}}\left( H,\ {{\mathbb{F}}_{p}} \right)$.

Keywords

12G0512G10cohomological dimensionSchreier's formulaGalois theoryp-extensionspro-p-groups
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 50 , Issue 4 , 01 December 2007 , pp. 588 - 593
Copyright
Copyright © Canadian Mathematical Society 2007

References

[K] Koch, H., Galois theory of p-extensions. Translated from the 1970 German original by Franz Lemmermeyer. With a postscript by the author and Lemmermeyer. Springer-Verlag, Berlin, 2002.Google Scholar
[LMS1] Lemire, N., Mináč, J., and Swallow, J., Galois module structure of Galois cohomology and partial Euler-Poincaré characteristics. To appear in J. Reine Angew. Math. ArXiv:math.NT/0409484, 2004.Google Scholar
[LMS2] Lemire, N., Mináč, J., and Swallow, J., When is Galois cohomology free or trivial. New York J. Math. 11(2005), 291–302.Google Scholar
[NSW] Neukirch, J., Schmidt, A., and Wingberg, K., Cohomology of number fields. Grundlehren der Mathematischen Wissenschaften 323, Springer-Verlag, Berlin, 2000.Google Scholar
[S1] Serre, J.-P., Galois cohomology. Springer-Verlag, Heidelberg, 1997.Google Scholar
[S2] Serre, J.-P., Sur la dimension cohomologique des groupes profinis. Topology 3(1965), 413–420.Google Scholar
[SJ] Suslin, A. and Joukhovitski, S., Norm varieties. J. Pure Appl. Algebra 206(2006), no. 1–2, 245–276.Google Scholar
[V1] Voevodsky, V., Motivic cohomology with ℤ/2-coefficients. Publ. Math. Inst. Hautes études Sci. no. 98 (2003), 59–104.Google Scholar
[V2] Voevodsky, V., On motivic cohomology with ℤ/l coefficients. K-theory preprint archive 639, 2003. http://www.math.uiuc.edu/K-theory/0639/.Google Scholar