Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T18:55:14.973Z Has data issue: false hasContentIssue false
  • English
  • Français

Coessential Abelianization Morphisms in the Category of Groups

Published online by Cambridge University Press:  20 November 2018

D. Oancea
D. Oancea*
Affiliation:
1549 Victoria St. E., Whitby, ON, L1N 9E3 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

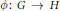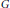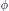An epimorphism $\phi :\,G\,\to \,H$ of groups, where $G$ has rank $n$, is called coessential if every (ordered) generating $n$-tuple of $H$ can be lifted along $\phi $ to a generating $n$-tuple for 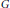$G$. We discuss this property in the context of the category of groups, and establish a criterion for such a group 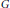$G$ to have the property that its abelianization epimorphism 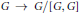$G\,\to \,{G}/{[G,G]}\;$, where 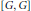$[G,\,G]$ is the commutator subgroup, is coessential. We give an example of a family of 2-generator groups whose abelianization epimorphism is not coessential. This family also provides counterexamples to the generalized Andrews–Curtis conjecture.

Keywords

20F0520F9920J15coessential epimorphismNielsen transformationsAndrew-Curtis transformations
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 2 , 01 June 2013 , pp. 395 - 399
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Adámek, J., Herrlich, H., and Strecker, G. E., Abstract and Concrete Categories; The Joy of Cats. Repr. Theory Appl. Categ. 17(2006), 1–507. Google Scholar
[2] Burns, R. G. and Oancea, D., Recalcitrance in groups II. J. Group Theory, Published online 12/05/2011. http://dx.doi.org/10.1515/JGT.2011.098 Google Scholar
[3] Diaconis, P. and Graham, R., The graph of generating sets of an abelian group. Colloq. Math. 80(1999), no. 1, 31–38. Google Scholar
[4] Gaschütz, W., Zu einem von B. H. und H. Neumann gestellten Problem. Math. Nachr. 14(1955), 249–252. http://dx.doi.org/10.1002/mana.19550140406 Google Scholar
[5] Dalla Volta, F. and A. Lucchini., Finite groups that need more generators than any proper quotient. J. Austral. Math. Soc. Ser. A 64(1998), no. 1, 82–91. http://dx.doi.org/10.1017/S1446788700001312 Google Scholar
[6] Oancea, D.. The Andrews-Curtis Conjecture and the Recalcitrance of Groups. Ph.D. Dissertation, York University, 2010.Google Scholar
[7] Oancea, D., A note on Nielsen equivalence in finitely generated abelian groups. Bull. Australian Math. Soc. 84(2011), 127–136. http://dx.doi.org/10.1017/S0004972711002279 Google Scholar
[8] Pride, S. J., On the Nielsen equivalence of pairs of generators in certain HNN groups. In: Proceedings of the Second International Conference on the Theory of Groups. Lecture Notes in Math. 372. Springer, Berlin, 1974, pp. 580–588.Google Scholar