Cliquishness and Quasicontinuity of Two-Variable Maps

Abstract

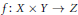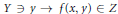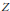We study the existence of continuity points for mappings $f\,:\,X\,\times \,Y\,\to \,Z$ whose $x$-sections $Y\,\backepsilon \,y\,\to \,f\left( x,y \right)\,\in \,Z$ are fragmentable and $y$-sections $X\,\backepsilon \,x\,\to \,f\left( x,y \right)\,\in \,Z$ are quasicontinuous, where $X$ is a Baire space and $Z$ is a metric space. For the factor 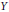$Y$, we consider two infinite “point-picking” games 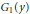${{G}_{1}}\,\left( y \right)$ and ${{G}_{2}}\,\left( y \right)$ defined respectively for each 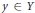$y\,\in \,Y$ as follows: in the $n$-th inning, Player I gives a dense set 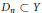${{D}_{n}}\,\subset \,Y$, respectively, a dense open set 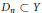${{D}_{n}}\,\subset \,Y$. Then Player II picks a point 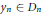${{y}_{n}}\,\in \,{{D}_{n}}$; II wins if $y$ is in the closure of 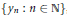$\left\{ {{y}_{n}}\,:\,n\,\in \,\mathbb{N} \right\}$, otherwise I wins. It is shown that (i) 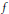$f$ is cliquish if II has a winning strategy in 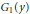${{G}_{1}}\,\left( y \right)$ for every 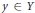$y\,\in \,Y$, and (ii) 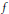$f$ is quasicontinuous if the $x$-sections of 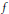$f$ are continuous and the set of 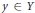$y\,\in \,Y$ such that II has a winning strategy in ${{G}_{2}}\,\left( y \right)$ is dense in 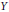$Y$. Item (i) extends substantially a result of Debs and item (ii) indicates that the problem of Talagrand on separately continuous maps has a positive answer for a wide class of “small” compact spaces.