Article contents
The Clifford-cyclotomic group and Euler–Poincaré characteristics
Published online by Cambridge University Press: 02 September 2020
Abstract
For an integer
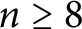 $n\geq 8$
divisible by
$n\geq 8$
divisible by
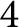 $4$
, let
$4$
, let
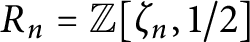 $R_n={\mathbb Z}[\zeta _n,1/2]$
and let
$R_n={\mathbb Z}[\zeta _n,1/2]$
and let
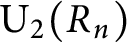 $\operatorname {\mathrm {U_{2}}}(R_n)$
be the group of
$\operatorname {\mathrm {U_{2}}}(R_n)$
be the group of
 $2\times 2$
unitary matrices with entries in
$2\times 2$
unitary matrices with entries in
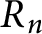 $R_n$
. Set
$R_n$
. Set
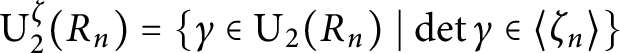 $\operatorname {\mathrm {U_2^\zeta }}(R_n)=\{\gamma \in \operatorname {\mathrm {U_{2}}}(R_n)\mid \det \gamma \in \langle \zeta _n\rangle \}$
. Let
$\operatorname {\mathrm {U_2^\zeta }}(R_n)=\{\gamma \in \operatorname {\mathrm {U_{2}}}(R_n)\mid \det \gamma \in \langle \zeta _n\rangle \}$
. Let
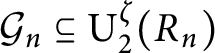 $\mathcal {G}_n\subseteq \operatorname {\mathrm {U_2^\zeta }}(R_n)$
be the Clifford-cyclotomic group generated by a Hadamard matrix
$\mathcal {G}_n\subseteq \operatorname {\mathrm {U_2^\zeta }}(R_n)$
be the Clifford-cyclotomic group generated by a Hadamard matrix
 $H=\frac {1}{2}[\begin {smallmatrix} 1+i & 1+i\\1+i &-1-i\end {smallmatrix}]$
and the gate
$H=\frac {1}{2}[\begin {smallmatrix} 1+i & 1+i\\1+i &-1-i\end {smallmatrix}]$
and the gate
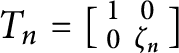 $T_n=[\begin {smallmatrix}1 & 0\\0 & \zeta _n\end {smallmatrix}]$
. We prove that
$T_n=[\begin {smallmatrix}1 & 0\\0 & \zeta _n\end {smallmatrix}]$
. We prove that
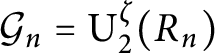 $\mathcal {G}_n=\operatorname {\mathrm {U_2^\zeta }}(R_n)$
if and only if
$\mathcal {G}_n=\operatorname {\mathrm {U_2^\zeta }}(R_n)$
if and only if
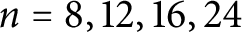 $n=8, 12, 16, 24$
and that
$n=8, 12, 16, 24$
and that
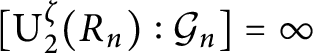 $[\operatorname {\mathrm {U_2^\zeta }}(R_n):\mathcal {G}_n]=\infty $
if
$[\operatorname {\mathrm {U_2^\zeta }}(R_n):\mathcal {G}_n]=\infty $
if
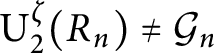 $\operatorname {\mathrm {U_2^\zeta }}(R_n)\neq \mathcal {G}_n$
. We compute the Euler–Poincaré characteristic of the groups
$\operatorname {\mathrm {U_2^\zeta }}(R_n)\neq \mathcal {G}_n$
. We compute the Euler–Poincaré characteristic of the groups
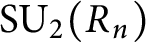 $\operatorname {\mathrm {SU_{2}}}(R_n)$
,
$\operatorname {\mathrm {SU_{2}}}(R_n)$
,
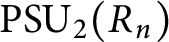 $\operatorname {\mathrm {PSU_{2}}}(R_n)$
,
$\operatorname {\mathrm {PSU_{2}}}(R_n)$
,
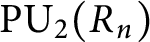 $\operatorname {\mathrm {PU_{2}}}(R_n)$
,
$\operatorname {\mathrm {PU_{2}}}(R_n)$
,
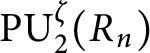 $\operatorname {\mathrm {PU_2^\zeta }}(R_n)$
, and
$\operatorname {\mathrm {PU_2^\zeta }}(R_n)$
, and
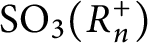 $\operatorname {\mathrm {SO_{3}}}(R_n^+)$
.
$\operatorname {\mathrm {SO_{3}}}(R_n^+)$
.
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2020
References
- 3
- Cited by



