Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T06:43:42.636Z Has data issue: false hasContentIssue false
  • English
  • Français

Classifying Spaces for Monoidal Categories Through Geometric Nerves

Published online by Cambridge University Press:  20 November 2018

M. Bullejos  and
A. M. Cegarra
M. Bullejos
Affiliation:
Departamento de Álgebra Facultad de Ciencias Universidad de Granada 18071 Granada, Spain, [email protected]
A. M. Cegarra
Affiliation:
Departamento de Álgebra Facultad de Ciencias Universidad de Granada 18071 Granada, Spain, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The usual constructions of classifying spaces for monoidal categories produce 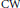$\text{CW}$-complexes with many cells that,moreover, do not have any proper geometric meaning. However, geometric nerves of monoidal categories are very handy simplicial sets whose simplices have a pleasing geometric description: they are diagrams with the shape of the 2-skeleton of oriented standard simplices. The purpose of this paper is to prove that geometric realizations of geometric nerves are classifying spaces for monoidal categories.

Keywords

18D1018G3055P1555P3555U40monoidal categorypseudo-simplicial categorysimplicial setclassifying spacehomotopy type
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 47 , Issue 3 , 01 September 2004 , pp. 321 - 331
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Bénabou, J., Introduction to bicategories. Reports of the Midwest Category Seminar, Springer, Berlin, 1967.Google Scholar
[2] Bousfield, A. K. and Kan, D. M., Homotopy limits, completions and localizations. Lecture Notes in Mathematics, 304, Springer, Berlin, 1972.Google Scholar
[3] Duskin, J., Simplicial matrices and nerves of weak n-categories, I: Nerves of bicategories. Theory Appl. Categ. 9 (2002), 198–308.Google Scholar
[4] Carrasco, P. and Cegarra, A. M., Braided Tensor structures on homotopy groupoids and nerves of (braided) categorical groups. Comm. Algebra 24 (1996), 3995–4058.Google Scholar
[5] Giraud, J., Cohomologie non abélienne. Grundlehren Math.Wiss. 179(1971).Google Scholar
[6] Gray, J. W., Fibred and Cofibred Categories. Proc. Conf. Categorical Algebra, Springer, New York, 1966 pp. 21–83.Google Scholar
[7] Grothendieck, A., Catégories fibrées et descente, S.G.A. I, Exposé VI. Lecture Notes in Mathematics, 224, Springer-Verlag, 1971).Google Scholar
[8] Hinich, V. A. and Schechtman, V. V., Geometry of a category of complexes and algebraic K-theory. Duke Math. J. 52 (1985), 339–430.Google Scholar
[9] Jardine, J. F., Supercoherence. J. Pure Appl. Algebra 75 (1991), 103–194.Google Scholar
[10] Joyal, A. and Street, R., Braided tensor categories. Adv. Math. 102 (1993), 20–78.Google Scholar
[11] Kan, D. M., On homotopy theory and c.s.s. groups. Ann. Math. 68 (1958), 38–53.Google Scholar
[12] Mac Lane, S., Categories for the working mathematician. Graduate Texts in Mathematics, 5, 2nd Edition, Springer, Berlin, 1998.Google Scholar
[13] May, J. P., Pairing of categories and spectra. J. Pure Appl. Algebra 19 (1980), 299–346.Google Scholar
[14] Quillen, D., Higher algebraic K-theory: I. In: Algebraic K-theory I, Lecture Notes in Mathematics, 341, Springer, Berlin, 1973, pp. 85–147.Google Scholar
[15] Thomason, R. W., Homotopy colimits in the category of small categories. Math. Proc. Camb. Phil. Soc. 85 (1979), 91–109.Google Scholar
[16] Segal, G. B., Classifying spaces and spectral sequences. Inst. Hautes ´Etudes Sci. Publ. Math. 34 (1968), 105–112.Google Scholar
[17] Segal, G. B., Categories and cohomology theories. Topology 13 (1974), 293–312.Google Scholar
[18] Street, R., Two constructions on lax functors. Cahiers Topologie Géometrie Différentielle 13 (1972), 217–264.Google Scholar
[19] Street, R., Categorical structures. In: Handbook of Algebra, Vol. I, North-Holland, Amsterdam, 1996, pp. 529–574.Google Scholar