No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
On a real hypersurface 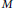 $M$ in a non-flat complex space form there exist the Levi–Civita and the
$M$ in a non-flat complex space form there exist the Levi–Civita and the  $k$-th generalized Tanaka–Webster connections. The aim of this paper is to study three dimensional real hypersurfaces in non-flat complex space forms, whose Lie derivative of the structure Jacobi operatorwith respect to the Levi–Civita connection coincides with the Lie derivative of it with respect to the
$k$-th generalized Tanaka–Webster connections. The aim of this paper is to study three dimensional real hypersurfaces in non-flat complex space forms, whose Lie derivative of the structure Jacobi operatorwith respect to the Levi–Civita connection coincides with the Lie derivative of it with respect to the  $k$-th generalized Tanaka-Webster connection. The Lie derivatives are considered in direction of the structure vector field and in direction of any vector field orthogonal to the structure vector field.
$k$-th generalized Tanaka-Webster connection. The Lie derivatives are considered in direction of the structure vector field and in direction of any vector field orthogonal to the structure vector field.