Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Vulakh, L. Ya.
1993.
Higher-dimensional analogues of Fuchsian subgroups of 𝑃𝑆𝐿(2,𝔬).
Transactions of the American Mathematical Society,
Vol. 337,
Issue. 2,
p.
947.
Vulakh, L. Ya.
1994.
Reflections in extended Bianchi groups.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 115,
Issue. 1,
p.
13.
Vulakh, L.
2000.
The Markov spectra for Fuchsian groups.
Transactions of the American Mathematical Society,
Vol. 352,
Issue. 9,
p.
4067.
VULAKH, L. YA.
2006.
DIOPHANTINE APPROXIMATION IN $\mathbf{Q}(\sqrt{-5})$ AND $\mathbf{Q}(\sqrt{-6})$.
International Journal of Number Theory,
Vol. 02,
Issue. 01,
p.
25.
VULAKH, L. YA
2010.
HERMITIAN POINTS IN MARKOV SPECTRA.
International Journal of Number Theory,
Vol. 06,
Issue. 04,
p.
713.
VULAKH, L. YA.
2010.
MINIMA OF BINARY INDEFINITE HERMITIAN FORMS.
International Journal of Number Theory,
Vol. 06,
Issue. 02,
p.
411.
Vulakh, L. Ya.
2012.
Diophantine approximation in $\mathbf{Q}(\sqrt{-30})$, $\mathbf{Q}(\sqrt{-33})$ and $\mathbf{Q}(\sqrt{-57})$.
Functiones et Approximatio Commentarii Mathematici,
Vol. 47,
Issue. 2,
Vulakh, L
2017.
Number Theory with an Emphasis on the Markoff Spectrum.
p.
297.
Yousaf, Awais
Alolaiyan, Hanan
Razaq, Abdul
and
Younis, Muhammad
2020.
Evolution of ambiguous numbers under the actions of a Bianchi group.
Journal of Taibah University for Science,
Vol. 14,
Issue. 1,
p.
615.


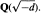 A complete classification of conjugacy classes of maximal non-elementary Fuchsian subgroups of PSL(2,
A complete classification of conjugacy classes of maximal non-elementary Fuchsian subgroups of PSL(2, 