Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T06:22:03.665Z Has data issue: false hasContentIssue false
  • English
  • Français

Classification of Integral Modular Categories of Frobenius–Perron Dimension pq4 and p2q2

Published online by Cambridge University Press:  20 November 2018

Paul Bruillard ,
Cásar Galindo ,
Seung-Moon Hong ,
Yevgenia Kashina ,
Deepak Naidu ,
Sonia Natale ,
Julia Yael Plavnik  and
Eric C. Rowell
Paul Bruillard
Affiliation:
Department of Mathematics, Texas A&M University, College Station, Texas 77843, USA e-mail: [email protected]
Cásar Galindo
Affiliation:
Departamento de Matemáticas, Universidad de los Andes, Bogotá, Colombia e-mail: [email protected]
Seung-Moon Hong
Affiliation:
Department of Mathematics and Statistics, University of Toledo, Ohio 43606, USA e-mail: [email protected]
Yevgenia Kashina
Affiliation:
Department of Mathematical Sciences, DePaul University, Chicago, Illinois 60614, USA e-mail: [email protected]
Deepak Naidu
Affiliation:
Department of Mathematical Sciences, Northern Illinois University, DeKalb, Illinois 60115, USA e-mail: [email protected]
Sonia Natale
Affiliation:
Facultad de Matemática, Astronomía y Física, Universidad Nacional de Córdoba, CIEM–CONICET, Córdoba, Argentina e-mail: [email protected]@famaf.unc.edu.ar
Julia Yael Plavnik
Affiliation:
Facultad de Matemática, Astronomía y Física, Universidad Nacional de Córdoba, CIEM–CONICET, Córdoba, Argentina e-mail: [email protected]@famaf.unc.edu.ar
Eric C. Rowell
Affiliation:
Department of Mathematics, Texas A & M University, College Station, Texas 77843, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

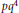We classify integral modular categories of dimension $p{{q}^{4}}$ and 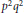${{p}^{2}}{{q}^{2}}$, where $p$ and $q$ are distinct primes. We show that such categories are always group-theoretical, except for categories of dimension 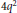$4{{q}^{2}}$. In these cases there are well-known examples of non-group-theoretical categories, coming from centers of Tambara–Yamagami categories and quantum groups. We show that a non-grouptheoretical integral modular category of dimension 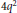$4{{q}^{2}}$ is either equivalent to one of these well-known examples or is of dimension 36 and is twist-equivalent to fusion categories arising froma certain quantum group.

Keywords

18D10modular categoriesfusion categories
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 4 , 01 December 2014 , pp. 721 - 734
Copyright
Copyright © Canadian Mathematical Society 2014

References

[DMNO] Davydov, A., M. M¨uger, Nikshych, D., and Ostrik, V., The Witt group of non-degenerate braided fusion categories.J. Reine Angew. Math. 677 (2013), 135–177.Google Scholar
[Ng] Dong, C., Lin, X., and Ng, S., Congruence property and galois symmetry of modular categories. arxiv:1201.6644.Google Scholar
[DGNO1] Drinfeld, V., Gelaki, S., Nikshych, D., and Ostrik, V., Group-theoretical properties of nilpotent modular categories. arxiv:0704.0195.Google Scholar
[DGNO2] Drinfeld, V., Gelaki, S., Nikshych, D., and Ostrik, V., On braided fusion categories. I. Selecta Math. (N. S.) 16 (2010), no. 1, 1–119. http://dx.doi.org/10.1007/s00029-010-0017-z Google Scholar
[EG] Etingof, P. and Gelaki, S., Some properties of finite-dimensional semisimple Hopf algebras.Math. Res. Lett. 5 (1998), no. 1–2, 191–197. http://dx.doi.org/10.4310/MRL.1998.v5.n2.a5 Google Scholar
[EGO] Etingof, P., Gelaki, S., and Ostrik, V., Classification of fusion categories of dimension pq.Int.Math. Res. Not. 2004, no. 57, 3041–3056.Google Scholar
[ENO1] Etingof, P., Nikshych, D., and Ostrik, V., On fusion categories.Ann. of Math. (2) 162 (2005), no. 2, 581–642. http://dx.doi.org/10.4007/annals.2005.162.581 Google Scholar
[ENO2] Etingof, P., Nikshych, D., and Ostrik, V., Weakly group-theoretical and solvable fusion categories.Adv. Math. 226 (2011), no. 1, 176–205. http://dx.doi.org/10.1016/j.aim.2010.06.009 Google Scholar
[ENO3] Etingof, P., Nikshych, D., and Ostrik, V., Fusion categories and homotopy theory.Quantum Topol. 1 (2010), no. 3, 209–273. http://dx.doi.org/10.4171/QT/6 Google Scholar
[ERW] Etingof, P., Rowell, E. C., and S. J.Witherspoon, Braid group representations from twisted quantum doubles of finite groups.Pacific J. Math. 234 (2008), no. 1, 33–41. http://dx.doi.org/10.2140/pjm.2008.234.33 Google Scholar
[G1] Galindo, C., Clifford theory for tensor categories.J. London Math. Soc. (2) 83 (2011), no. 1, 57–78. http://dx.doi.org/10.1112/jlms/jdq064 Google Scholar
[G2] Galindo, C., Clifford theory for graded fusion categories.Israel J. Math. 192 (2012), no. 2, 841–867. http://dx.doi.org/10.1007/s11856-012-0055-7 Google Scholar
[GHR] Galindo, C., Hong, S.-M., and Rowell, E. C., Generalized and quasi-localizations of braid group representations.Int. Math. Res. Not. 2013, no. 3, 693–731.Google Scholar
[GNN] Gelaki, S., Naidu, D., and Nikshych, D., Centers of graded fusion categories.Algebra Number Theory 3 (2009), no. 8, 959–990. http://dx.doi.org/10.2140/ant.2009.3.959 Google Scholar
[GN] Gelaki, S. and Nikshych, D., Nilpotent fusion categories.Adv. Math. 217 (2008), no. 3, 1053–1071. http://dx.doi.org/10.1016/j.aim.2007.08.001 Google Scholar
[JL] Jordan, D. and Larson, E., On the classification of certain fusion categories. J. Noncommut. Geom. 3 (2009), no. 3, 481–499. http://dx.doi.org/10.4171/JNCG/44 Google Scholar
[KW] Kazhdan, D. and H.Wenzl, Reconstructing monoidal categories. In: I. M. Gelfand Seminar, Adv. Soviet Math., 16, Part 2, American Mathematical Society, Providence, RI, 1993, pp. 111–136.Google Scholar
[K] Kirillov, A., Jr., Modular categories and orbifold models. II. arxiv:math/0110221.Google Scholar
[M1] Müger, M., Galois theory for braided tensor categories and the modular closure.Adv. Math. 150 (2000), no. 2, 151–201. http://dx.doi.org/10.1006/aima.1999.1860 Google Scholar
[M2] Müger, M., On the structure of modular categories.Proc. London Math. Soc. 87 (2003), no. 2, 291–308. http://dx.doi.org/10.1112/S0024611503014187 Google Scholar
[M3] Müger, M., Galois extensions of braided tensor categories and braided crossed G-categories.J. Algebra 277 (2004), no. 1, 256–281. http://dx.doi.org/10.1016/j.jalgebra.2004.02.026 Google Scholar
[NNW] Naidu, D., Nikshych, D., and S.Witherspoon, Fusion subcategories of representation categories of twisted quantum doubles of finite groups.Int. Math. Res. Not. 2009, no. 22, 4183–4219.Google Scholar
[NR] Naidu, D. and Rowell, E. C., A finiteness property for braided fusion categories.Algebr. Represent. Theory. 14 (2011), no. 5, 837–855. http://dx.doi.org/10.1007/s10468-010-9219-5 Google Scholar
[Na1] Natale, S., On group theoretical Hopf algebras and exact factorizations of finite groups.J. Algebra 270 (2003), no. 1, 199–211. http://dx.doi.org/10.1016/S0021-8693(03)00464-2 Google Scholar
[Na2] Natale, S., On weakly group-theoretical non-degenerate braided fusion categories. arxiv:1301.6078.Google Scholar
[O] Ostrik, V., Module categories over the Drinfeld double of a finite group.Int. Math. Res. Not. 2003, no. 27, 1507–1520.Google Scholar