Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-28T01:22:27.510Z Has data issue: false hasContentIssue false
  • English
  • Français

Classification of AF Flows

Published online by Cambridge University Press:  20 November 2018

Andrew J. Dean
Andrew J. Dean*
Affiliation:
Department of Mathematical Sciences, Lakehead University, 955 Oliver Road, Thunder Bay, Ontario P7B 5E1, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An 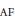$\text{AF}$ flow is a one-parameter automorphism group of an 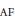$\text{AF}$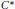${{C}^{*}}$-algebra 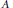$A$ such that there exists an increasing sequence of invariant finite dimensional sub-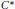${{C}^{*}}$-algebras whose union is dense in 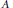$A$. In this paper, a classification of 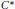${{C}^{*}}$-dynamical systems of this form up to equivariant isomorphism is presented. Two pictures of the actions are given, one in terms of a modified Bratteli diagram/pathspace construction, and one in terms of a modified 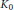${{K}_{0}}$ functor.

Keywords

46L5746L35
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 46 , Issue 2 , 01 June 2003 , pp. 164 - 177
Copyright
Copyright © Canadian Mathematical Society 2003

References

[1] Bratteli, O., Inductive limits of finite dimensional C*-algebras. Trans. Amer. math. Soc. 171 (1972), 195–234.Google Scholar
[2] Bratteli, O., Elliott, G. A., Evans, D. E. and Kishimoto, A., On the classification of inductive limits of inner actions of a compact group. Current topics in operator algebras, Nara, 1990, 13–24, World Scientific Publishing, River Edge, New Jersey, 1991.Google Scholar
[3] Dean, A. J., An invariant for actions of R on UHF C*-algebras. C. R. Math. Rep. Acad. Sci. Canada (3) 23 (2001), 91–96.Google Scholar
[4] Elliott, G. A., On the classification of inductive limits of sequences of semi simple finite-dimensional algebras. J. Algebra 38 (1976), 29–44.Google Scholar
[5] Elliott, G. A., On the classification of C*-algebras of real rank zero. J. Reine Angew.Math. 443 (1993), 179–219.Google Scholar
[6] Elliott, G. A. and Su, H., K-theoretic classification for inductive limit Z2 actions on AF algebras. Canad. J. Math. 48 (1996), 946–958.Google Scholar
[7] Evans, D. E. and Kawahigashi, Y., Quantum Symmetries on Operator Algebras. Oxford University Press, 1998.Google Scholar
[8] Handelman, D. and Rossmann, W., Product type actions of finite and compact groups. Indiana Univ. Math. J. 33 (1984), 479–509.Google Scholar
[9] Handelman, D. and Rossmann, W., Actions of compact groups on AF C*-algebras. Illinois J. Math. 29 (1985), 51–95.Google Scholar
[10] Kishimoto, A., Actions of finite groups on certain inductive limit C*-algebras. Internat. J. Math. (3) 1 (1990), 267–292.Google Scholar
[11] Sakai, S., Operator algebras in dynamical systems. Cambridge University Press, 1991.Google Scholar
[12] Takesaki, M., Theory of Operator Algebras I. Springer-Verlag, New York, Heidelberg, Berlin, 1979.Google Scholar