Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mollin, R. A.
and
Williams, H. C.
1995.
Proof, Disproof and Advances Concerning Certain Conjectures on Real Quadratic Fields .
Canadian Journal of Mathematics,
Vol. 47,
Issue. 5,
p.
1023.
KOBAYASHI, Masaki
1995.
On generators of ideal class groups in quadratic fields.
Japanese journal of mathematics. New series,
Vol. 21,
Issue. 1,
p.
105.


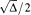 where Δ is the discriminant of
where Δ is the discriminant of 