Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-20T16:24:33.333Z Has data issue: false hasContentIssue false
  • English
  • Français

A Class of Addition Theorems†

Published online by Cambridge University Press:  20 November 2018

H. M. Srivastava ,
J.-L. Lavoie  and
Richard Tremblay
H. M. Srivastava
Affiliation:
Department of MathematicsUniversity of VictoriaVictoria V8w 2Y2Canada
J.-L. Lavoie
Affiliation:
Département Des Mathématiques, Université LavalQuébec G1K 7P4, Canada
Richard Tremblay
Affiliation:
Department des Sciences Économiques, Université du QuébecChicoutimi Québec G7H 2P9, Canada
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Recently, H. M. Srivastava extended certain interesting generating functions of L. Carlitz to the forms:

and

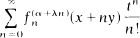
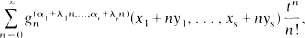
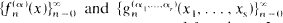where are general oncand many-parameter sequences of functions. In the present paper some general addition formulas for analogous sequences of functions are derived, and a number of interesting applications of the main results are given.

Keywords

33A6533A70Secondary 10A40Generating functionsaddition formulasTaylor's theoremLeibniz's formulaBernoulli polynomialsEuler polynomialsHermite polynomialsLaguerre polynomialsbiorthogonal polynomialsTaylor's seriesLagrange's expansion theorem.
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 26 , Issue 4 , 01 December 1983 , pp. 438 - 445
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. Carlitz, L., A class of generating functions, SIAM J. Math. Anal. 8 (1977), 518-532.Google Scholar
2. Konhauser, J. D. E., Biorthogonal polynomials suggested by the Laguerre polynomials, Pacific J. Math. 21 (1967), 303-314.Google Scholar
3. Osier, T. J., The fractional derivative of a composite function, SIAM J. Math. Anal. 1 (1970), 288-293.Google Scholar
4. Srivastava, H. M., Some generalizations of Carlitz's theorem, Pacific J. Math. 85 (1979), 471-477.Google Scholar
5. Srivastava, H. M. and Singhal, J. P., A class of polynomials defined by generalized Rodrigues' formula, Ann. Mat. Pura Appl. (4) 90 (1971), 75-85.Google Scholar
6. Whittaker, E. T. and Watson, G. N., A Course of Modern Analysis, Fourth edition, Cambridge University Press, London and New York, 1927.Google Scholar