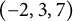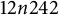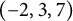1 Introduction
Given a knot
![]() $K\subseteq S^3$
, we say that
$K\subseteq S^3$
, we say that
![]() $p/q\in \mathbb {Q}$
is a characterizing slope for K if the oriented homeomorphism type of the manifold obtained by
$p/q\in \mathbb {Q}$
is a characterizing slope for K if the oriented homeomorphism type of the manifold obtained by
![]() $p/q$
-surgery on K determines the isotopy type of K uniquely. That is,
$p/q$
-surgery on K determines the isotopy type of K uniquely. That is,
![]() $p/q$
is a characterizing slope for K if there does not exist any knot
$p/q$
is a characterizing slope for K if there does not exist any knot
![]() $K'\neq K$
such that
$K'\neq K$
such that
![]() $S^3_{p/q}(K)\cong S^3_{p/q}(K')$
. It was shown by Lackenby that every knot admits infinitely many characterizing slopes and for a hyperbolic knot any slope
$S^3_{p/q}(K)\cong S^3_{p/q}(K')$
. It was shown by Lackenby that every knot admits infinitely many characterizing slopes and for a hyperbolic knot any slope
![]() $p/q$
with q sufficiently large is characterizing [Reference LackenbyLac19]. Although these results show the existence of characterizing slopes, the proofs are nonconstructive and so there are very few hyperbolic knots for which explicit examples of characterizing slopes are known. Ozsváth and Szabó have shown that every slope is characterizing for the figure-eight knot
$p/q$
with q sufficiently large is characterizing [Reference LackenbyLac19]. Although these results show the existence of characterizing slopes, the proofs are nonconstructive and so there are very few hyperbolic knots for which explicit examples of characterizing slopes are known. Ozsváth and Szabó have shown that every slope is characterizing for the figure-eight knot
![]() $4_1$
[Reference Ozsváth and SzabóOS19], and recent work of Baldwin and Sivek implies that every noninteger slope is characterizing for
$4_1$
[Reference Ozsváth and SzabóOS19], and recent work of Baldwin and Sivek implies that every noninteger slope is characterizing for
![]() $5_2$
[Reference Baldwin and SivekBS22]. The aim of this article is to exhibit explicit examples of characterizing slopes for the knot
$5_2$
[Reference Baldwin and SivekBS22]. The aim of this article is to exhibit explicit examples of characterizing slopes for the knot
![]() $12n242$
, also known as the
$12n242$
, also known as the
![]() $(-2,3,7)$
-pretzel knot (see Figure 1). Since
$(-2,3,7)$
-pretzel knot (see Figure 1). Since
![]() $12n242$
is a hyperbolic L-space knot—Fintushel and Stern showed that it admits two lens space surgeries [Reference Fintushel and SternFS80]—it has only finitely many noncharacterizing slopes that are not negative integers [Reference McCoyMcC19]. The following theorem is a quantitative version of this fact. As far as the author is aware, these are the first known explicit examples of characterizing slopes on a hyperbolic knot with genus greater than one.
$12n242$
is a hyperbolic L-space knot—Fintushel and Stern showed that it admits two lens space surgeries [Reference Fintushel and SternFS80]—it has only finitely many noncharacterizing slopes that are not negative integers [Reference McCoyMcC19]. The following theorem is a quantitative version of this fact. As far as the author is aware, these are the first known explicit examples of characterizing slopes on a hyperbolic knot with genus greater than one.
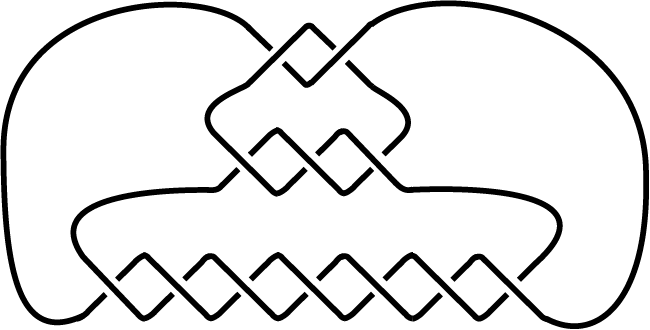
Figure 1 The main protagonist:
![]() $12n242$
.
$12n242$
.
Theorem 1.1 Any slope
![]() $p/q$
satisfying at least one of the following conditions is a characterizing slope for
$p/q$
satisfying at least one of the following conditions is a characterizing slope for
![]() $12n242$
:
$12n242$
:
-
(i)
 $q\geq 49$
;
$q\geq 49$
; -
(ii)
 $p\geq \max \{24q, 441\}$
; or
$p\geq \max \{24q, 441\}$
; or -
(iii)
 $q\geq 2$
and
$q\geq 2$
and
 $p\leq - \max \{12+4q^2-2q,441 \}$
.
$p\leq - \max \{12+4q^2-2q,441 \}$
.
Note that Theorem 1.1 also yields information about the characterizing slopes of the mirror of
![]() $12n242$
: a slope
$12n242$
: a slope
![]() $p/q$
is characterizing for a knot K if and only if
$p/q$
is characterizing for a knot K if and only if
![]() $-p/q$
is characterizing for the mirror
$-p/q$
is characterizing for the mirror
![]() $mK$
. The key input allowing us to prove Theorem 1.1 is the fact that
$mK$
. The key input allowing us to prove Theorem 1.1 is the fact that
![]() $12n242$
is one of the knots with smallest volume (up to reflection it one of only three hyperbolic knots with volume smaller than 3.07) [Reference Gabai, Haraway, Meyerhoff, Thurston and YarmolaGHM21]. A result of Futer, Kalfagianni, and Purcell on the change in volume of a hyperbolic manifold under Dehn filling [Reference Futer, Kalfagianni and PurcellFKP08] can then be used to restrict potential noncharacterizing slopes coming from surgeries on hyperbolic knots with large volume (and satellites thereof). This leaves only the possibility of noncharacterizing slopes coming from surgeries on the other knots of small volume, explicitly
$12n242$
is one of the knots with smallest volume (up to reflection it one of only three hyperbolic knots with volume smaller than 3.07) [Reference Gabai, Haraway, Meyerhoff, Thurston and YarmolaGHM21]. A result of Futer, Kalfagianni, and Purcell on the change in volume of a hyperbolic manifold under Dehn filling [Reference Futer, Kalfagianni and PurcellFKP08] can then be used to restrict potential noncharacterizing slopes coming from surgeries on hyperbolic knots with large volume (and satellites thereof). This leaves only the possibility of noncharacterizing slopes coming from surgeries on the other knots of small volume, explicitly
![]() $4_1, 5_2, m5_2$
and
$4_1, 5_2, m5_2$
and
![]() $m12n242$
, or satellites of these knots. Alongside tools from hyperbolic geometry, we use the Casson–Walker invariant and the
$m12n242$
, or satellites of these knots. Alongside tools from hyperbolic geometry, we use the Casson–Walker invariant and the
![]() $\nu ^+$
invariant from Heegaard Floer homology to rule out such surgeries.
$\nu ^+$
invariant from Heegaard Floer homology to rule out such surgeries.
In principle, one could use a similar approach to derive information about the characterizing slopes of the other small volume knots:
![]() $4_1$
and
$4_1$
and
![]() $5_2$
. However, much better results have already been obtained by other means for both of these knots [Reference Baldwin and SivekBS22, Reference Ozsváth and SzabóOS19], so we restrict our analysis to
$5_2$
. However, much better results have already been obtained by other means for both of these knots [Reference Baldwin and SivekBS22, Reference Ozsváth and SzabóOS19], so we restrict our analysis to
![]() $12n242$
.
$12n242$
.
We note that Theorem 1.1 says nothing about negative integer characterizing slope. Although there are knots which possess infinitely many integer noncharacterizing slopes [Reference Baker and MotegiBM18], all known examples admit infinitely many noncharacterizing slopes of both sign. This suggests that
![]() $12n242$
(and L-space knots more generally) should admit only finitely many integer noncharacterizing slopes. However, establishing such a result remains an interesting and challenging problem.
$12n242$
(and L-space knots more generally) should admit only finitely many integer noncharacterizing slopes. However, establishing such a result remains an interesting and challenging problem.
1.1 Noncharacterizing slopes
Lackenby has shown for a hyperbolic knot K any slope
![]() $p/q$
with q sufficiently large is characterizing for K [Reference LackenbyLac19]. For example, Theorem 1.1 shows that
$p/q$
with q sufficiently large is characterizing for K [Reference LackenbyLac19]. For example, Theorem 1.1 shows that
![]() $q\geq 49$
is sufficiently large for
$q\geq 49$
is sufficiently large for
![]() $12n242$
. However, the “sufficiently large” here is inherently dependant on the specific knot in question. To illustrate this dependence, we exhibit a family of hyperbolic two-bridge knots
$12n242$
. However, the “sufficiently large” here is inherently dependant on the specific knot in question. To illustrate this dependence, we exhibit a family of hyperbolic two-bridge knots
![]() $\{K_q\}_{q\geq 1}$
such that for each q, the slope
$\{K_q\}_{q\geq 1}$
such that for each q, the slope
![]() $\frac {1}{q}$
is noncharacterizing for
$\frac {1}{q}$
is noncharacterizing for
![]() $K_q$
. This family is shown in Figure 2. The construction given is essentially the same as the one used by Brakes to find examples of surgeries on distinct satellite knots yielding the same manifold [Reference BrakesBra80].
$K_q$
. This family is shown in Figure 2. The construction given is essentially the same as the one used by Brakes to find examples of surgeries on distinct satellite knots yielding the same manifold [Reference BrakesBra80].
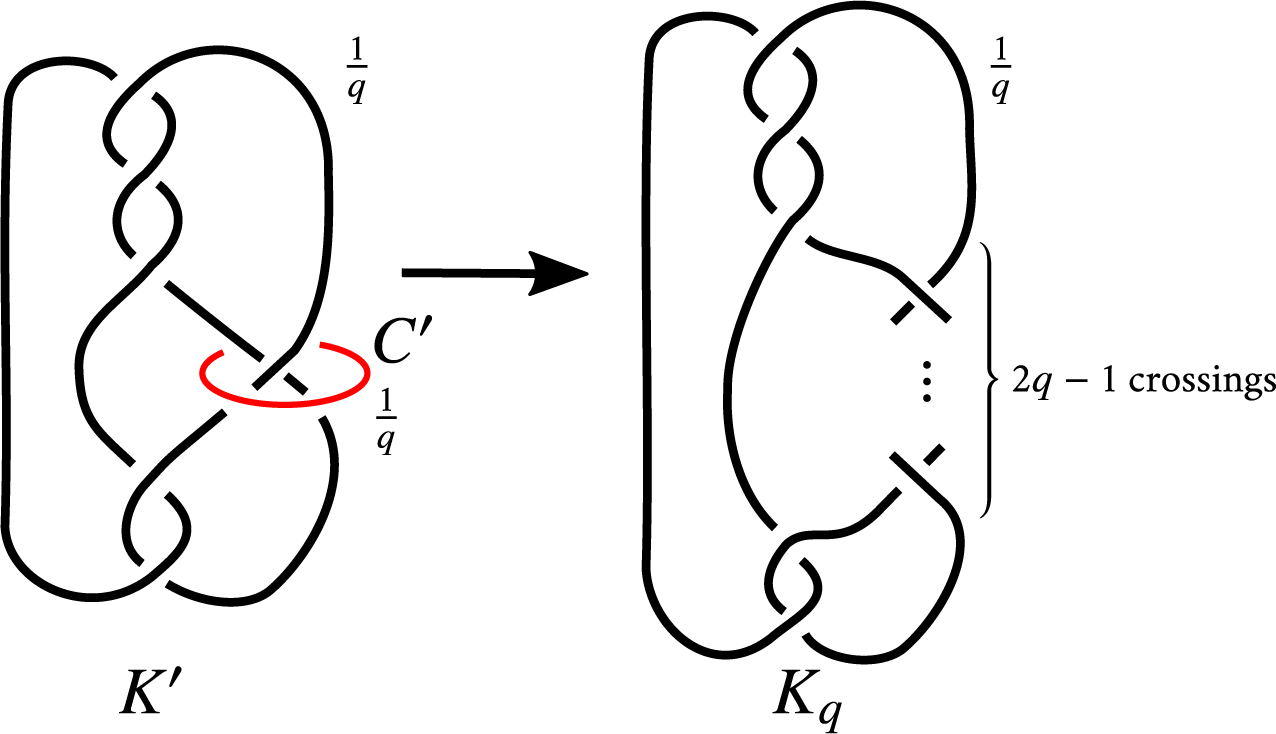
Figure 2 A link
![]() $K'\cup C'$
, such that twisting along
$K'\cup C'$
, such that twisting along
![]() $C'$
yields the two-bridge link
$C'$
yields the two-bridge link
![]() $K_q$
. Proposition 4.1 implies that
$K_q$
. Proposition 4.1 implies that
![]() $K_q$
has
$K_q$
has
![]() $\frac {1}{q}$
as a noncharacterizing slope.
$\frac {1}{q}$
as a noncharacterizing slope.
1.2 Conventions
The following notational conventions will be in force throughout the paper:
-
• Knots are always considered up to isotopy.
-
• When considering a rational number
 $p/q\in \mathbb {Q}$
, we will always assume this to be written with p and q coprime and
$p/q\in \mathbb {Q}$
, we will always assume this to be written with p and q coprime and
 $q\geq 1$
.
$q\geq 1$
. -
• When performing Dehn surgery on a knot K, we use
 $p/q$
to denote the slope
$p/q$
to denote the slope
 ${p\mu +q\lambda }$
, where
${p\mu +q\lambda }$
, where
 $\mu $
is the meridian and
$\mu $
is the meridian and
 $\lambda $
is the null-homologous longitude.
$\lambda $
is the null-homologous longitude. -
• Given two oriented 3-manifolds Y and
 $Y'$
, we will use
$Y'$
, we will use
 $Y\cong Y'$
to denote the existence of an orientation-preserving homeomorphism between them.
$Y\cong Y'$
to denote the existence of an orientation-preserving homeomorphism between them. -
• For a knot K, we will denote its Alexander polynomial by
 $\Delta _{K}(t)$
. We will always assume this is normalized so that
$\Delta _{K}(t)$
. We will always assume this is normalized so that
 $\Delta _{K}(1)=1$
and
$\Delta _{K}(1)=1$
and
 $\Delta _K(t)=\Delta _K(t^{-1})$
.
$\Delta _K(t)=\Delta _K(t^{-1})$
. -
• Given a knot K in
 $S^3$
, we will use
$S^3$
, we will use
 $mK$
to denote its mirror.
$mK$
to denote its mirror. -
• An L-space knot is one which admits positive L-space surgeries.
2 Preliminaries
In this section, we gather together all the auxiliary results required for the proof of Theorem 1.1.
2.1 Knots of small volume
First, we use the fact that Gabai, Haraway, Meyerhoff, Thurston, and Yarmola have classified the hyperbolic 3-manifolds of small volume [Reference Gabai, Haraway, Meyerhoff, Thurston and YarmolaGHM21].
Theorem 2.1 If K is a hyperbolic knot in
![]() $S^3$
with
$S^3$
with
![]() $\mathrm {vol}(K)\leq 3.07$
, then
$\mathrm {vol}(K)\leq 3.07$
, then
Proof Gabai, Haraway, Meyerhoff, Thurston, and Yarmola have shown that there are exactly 14 one-cusped orientable hyperbolic 3-manifolds with hyperbolic volume less than or equal to 3.07 and that these are
![]() $\mathtt {m003}$
,
$\mathtt {m003}$
,
![]() $\mathtt {m004}$
,
$\mathtt {m004}$
,
![]() $\mathtt {m006}$
,
$\mathtt {m006}$
,
![]() $\mathtt {m007}$
,
$\mathtt {m007}$
,
![]() $\mathtt {m009}$
,
$\mathtt {m009}$
,
![]() $\mathtt {m010}$
,
$\mathtt {m010}$
,
![]() $\mathtt {m011}$
,
$\mathtt {m011}$
,
![]() $\mathtt {m015}$
,
$\mathtt {m015}$
,
![]() $\mathtt {m016}$
,
$\mathtt {m016}$
,
![]() $\mathtt {m017}$
,
$\mathtt {m017}$
,
![]() $\mathtt {m019}$
,
$\mathtt {m019}$
,
![]() $\mathtt {m022}$
,
$\mathtt {m022}$
,
![]() $\mathtt {m023}$
, and
$\mathtt {m023}$
, and
![]() $\mathtt {m026}$
[Reference Gabai, Haraway, Meyerhoff, Thurston and YarmolaGHM21, Theorem 1.5]. Precisely, three of these arise as the complements of knots in
$\mathtt {m026}$
[Reference Gabai, Haraway, Meyerhoff, Thurston and YarmolaGHM21, Theorem 1.5]. Precisely, three of these arise as the complements of knots in
![]() $S^3$
:
$S^3$
:
![]() $\mathtt {m004}$
,
$\mathtt {m004}$
,
![]() $\mathtt {m015}$
, and
$\mathtt {m015}$
, and
![]() $\mathtt {m016}$
are (ignoring orientations) the complements of
$\mathtt {m016}$
are (ignoring orientations) the complements of
![]() $4_1$
,
$4_1$
,
![]() $5_2$
, and
$5_2$
, and
![]() $12n242$
, respectively.
$12n242$
, respectively.
We will informally refer to the five knots in Theorem 2.1 as the “low volume knots” and the remaining hyperbolic knots as the “large volume knots.” For our purposes, it will be useful to note that the volume of
![]() $4_1$
satisfies
$4_1$
satisfies
and the volume of
![]() $12n242$
satisfies
$12n242$
satisfies
2.2 Slope lengths
Let K be a hyperbolic knot in
![]() $S^3$
, that is,
$S^3$
, that is,
![]() $S^3\setminus K$
admits a complete finite-volume hyperbolic structure with one cusp. Given a slope
$S^3\setminus K$
admits a complete finite-volume hyperbolic structure with one cusp. Given a slope
![]() $\sigma $
on K and horoball neighborhood N of the cusp, we can assign a length to
$\sigma $
on K and horoball neighborhood N of the cusp, we can assign a length to
![]() $\sigma $
by considering the minimal length of a curve representing
$\sigma $
by considering the minimal length of a curve representing
![]() $\sigma $
on
$\sigma $
on
![]() $\partial N$
(measured in the natural Euclidean metric on
$\partial N$
(measured in the natural Euclidean metric on
![]() $\partial N$
). Since
$\partial N$
). Since
![]() $S^3\setminus K$
has a unique cusp, there is a unique maximal horoball neighborhood of this cusp. We will use
$S^3\setminus K$
has a unique cusp, there is a unique maximal horoball neighborhood of this cusp. We will use
![]() $\ell _K(\sigma )$
to denote the length of
$\ell _K(\sigma )$
to denote the length of
![]() $\sigma $
with respect this maximal horoball neighborhood.
$\sigma $
with respect this maximal horoball neighborhood.
Lemma 2.2 Let K and
![]() $K'$
be hyperbolic knots in
$K'$
be hyperbolic knots in
![]() $S^3$
with
$S^3$
with
![]() $\mathrm {vol}(K')<\mathrm {vol}(K)$
. If r and
$\mathrm {vol}(K')<\mathrm {vol}(K)$
. If r and
![]() $r'$
are slopes such that
$r'$
are slopes such that
![]() $S_{r}^3(K)\cong S_{r'}^3(K')$
, then
$S_{r}^3(K)\cong S_{r'}^3(K')$
, then
 $$\begin{align*}\ell_{K}(r)<\frac{2\pi}{\sqrt{1-\left(\frac{\mathrm{vol}(K')}{\mathrm{vol}(K)}\right)^{\frac23}}}. \end{align*}$$
$$\begin{align*}\ell_{K}(r)<\frac{2\pi}{\sqrt{1-\left(\frac{\mathrm{vol}(K')}{\mathrm{vol}(K)}\right)^{\frac23}}}. \end{align*}$$
Proof Since the bound on the right-hand side is always strictly greater then
![]() $2\pi $
, we can assume without loss of generality that
$2\pi $
, we can assume without loss of generality that
![]() $\ell =\ell _{K}(r)>2\pi $
. By Perelman’s resolution of the geometrization conjecture [Reference PerelmanPer02, Reference PerelmanPer03a, Reference PerelmanPer03b] and the
$\ell =\ell _{K}(r)>2\pi $
. By Perelman’s resolution of the geometrization conjecture [Reference PerelmanPer02, Reference PerelmanPer03a, Reference PerelmanPer03b] and the
![]() $2\pi $
-theorem [Reference Bleiler and HodgsonBH96], this implies that
$2\pi $
-theorem [Reference Bleiler and HodgsonBH96], this implies that
![]() $S_{r}^3(K)$
is a hyperbolic manifold. Furthermore, Futer, Kalfagianni, and Purcell have shown that we have the following volume bound [Reference Futer, Kalfagianni and PurcellFKP08, Theorem 1.1]:
$S_{r}^3(K)$
is a hyperbolic manifold. Furthermore, Futer, Kalfagianni, and Purcell have shown that we have the following volume bound [Reference Futer, Kalfagianni and PurcellFKP08, Theorem 1.1]:
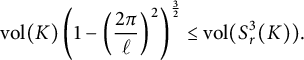 $$\begin{align*}\mathrm{vol}(K)\left(1- \left(\frac{2\pi}{\ell}\right)^2\right)^{\frac32}\leq\mathrm{vol}(S_{r}^3(K)). \end{align*}$$
$$\begin{align*}\mathrm{vol}(K)\left(1- \left(\frac{2\pi}{\ell}\right)^2\right)^{\frac32}\leq\mathrm{vol}(S_{r}^3(K)). \end{align*}$$
Moreover, since Thurston showed that volume strictly decreases under hyperbolic Dehn filling [Reference ThurstonThu80, Theorem 6.5.6], we have that
![]() $\mathrm {vol}(S_{r}^3(K))=\mathrm {vol}(S_{r'}^3(K'))<\mathrm {vol}(K')$
. Together these bounds give
$\mathrm {vol}(S_{r}^3(K))=\mathrm {vol}(S_{r'}^3(K'))<\mathrm {vol}(K')$
. Together these bounds give
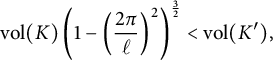 $$\begin{align*}\mathrm{vol}(K)\left(1- \left(\frac{2\pi}{\ell}\right)^2\right)^{\frac32}<\mathrm{vol}(K'), \end{align*}$$
$$\begin{align*}\mathrm{vol}(K)\left(1- \left(\frac{2\pi}{\ell}\right)^2\right)^{\frac32}<\mathrm{vol}(K'), \end{align*}$$
which can be easily rearranged to give the desired bound on
![]() $\ell _K(p/q)$
.
$\ell _K(p/q)$
.
Next, we need a mechanism for converting bounds on
![]() $\ell _K(p/q)$
into bounds on p and q.
$\ell _K(p/q)$
into bounds on p and q.
Lemma 2.3 Let
![]() $K\subseteq S^3$
be a hyperbolic knot of genus
$K\subseteq S^3$
be a hyperbolic knot of genus
![]() $g(K)$
. Then:
$g(K)$
. Then:
-
(a)
 $|q|\leq 1.79 \ell _K(p/q)$
and
$|q|\leq 1.79 \ell _K(p/q)$
and -
(b)
 $|p|\leq 1.79\ell _K(p/q)(2g(K)-1).$
$|p|\leq 1.79\ell _K(p/q)(2g(K)-1).$
Proof Let N be a horocusp neighborhood in the complement
![]() $S^3\setminus K$
of K. Let A be the area of
$S^3\setminus K$
of K. Let A be the area of
![]() $\partial N$
(equipped with its Euclidean metric). A simple geometric argument (e.g., as used by Cooper and Lackenby [Reference Cooper and LackenbyCL98, Lemma 2.1]) shows that for any two slopes of K, we have
$\partial N$
(equipped with its Euclidean metric). A simple geometric argument (e.g., as used by Cooper and Lackenby [Reference Cooper and LackenbyCL98, Lemma 2.1]) shows that for any two slopes of K, we have
where
![]() $\Delta (\alpha ,\beta )$
denotes the distance between
$\Delta (\alpha ,\beta )$
denotes the distance between
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
(cf. [Reference AgolAgo00, Lemma 8.1]). Since Cao and Meyerhoff have shown there always exists a horocusp neighborhood N with
$\beta $
(cf. [Reference AgolAgo00, Lemma 8.1]). Since Cao and Meyerhoff have shown there always exists a horocusp neighborhood N with
![]() $\mathrm {Area}(\partial N)\geq 3.35$
[Reference Cao and Robert MeyerhoffCM01], this establishes the bound
$\mathrm {Area}(\partial N)\geq 3.35$
[Reference Cao and Robert MeyerhoffCM01], this establishes the bound
for all slopes
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. Since
$\beta $
. Since
![]() $\Delta (1/0,p/q)=|q|$
and
$\Delta (1/0,p/q)=|q|$
and
![]() $\ell _K(1/0)\leq 6$
by the 6-theorem of Agol and Lackenby [Reference AgolAgo00, Reference LackenbyLac03], this gives the bound (a). Since
$\ell _K(1/0)\leq 6$
by the 6-theorem of Agol and Lackenby [Reference AgolAgo00, Reference LackenbyLac03], this gives the bound (a). Since
![]() $\Delta (0/1,p/q)=|p|$
and
$\Delta (0/1,p/q)=|p|$
and
![]() $\ell _K(0/1)\leq 6(2g-1)$
by [Reference AgolAgo00, Theorem 5.1], this also gives the bound (b).
$\ell _K(0/1)\leq 6(2g-1)$
by [Reference AgolAgo00, Theorem 5.1], this also gives the bound (b).
2.3 Hyperbolic surgeries on satellite knots
We will use the following result to understand noncharacterizing slopes coming from satellite knots.
Lemma 2.4 Let K be a satellite knot such that
![]() $S_{p/q}^3(K)$
is hyperbolic for some
$S_{p/q}^3(K)$
is hyperbolic for some
![]() ${p/q\in \mathbb {Q}}$
. Then there is a hyperbolic knot J with
${p/q\in \mathbb {Q}}$
. Then there is a hyperbolic knot J with
![]() $g(J)<g(K)$
and an integer
$g(J)<g(K)$
and an integer
![]() $w>1$
such that
$w>1$
such that
![]() $S_{p/q}^3(K)\cong S_{p/(qw^2)}^3(J)$
. Moreover, if
$S_{p/q}^3(K)\cong S_{p/(qw^2)}^3(J)$
. Moreover, if
![]() $q\geq 2$
, then K is a cable of J with winding number w.
$q\geq 2$
, then K is a cable of J with winding number w.
Proof Let T be an incompressible torus in
![]() $S^3\setminus K$
. We can consider K as a knot in the solid torus V bounded by T. Thus, we can consider K as a satellite with companion given by the core J of V. By choosing T to be “innermost,” we can ensure that
$S^3\setminus K$
. We can consider K as a knot in the solid torus V bounded by T. Thus, we can consider K as a satellite with companion given by the core J of V. By choosing T to be “innermost,” we can ensure that
![]() $S^3\setminus J$
contains no further incompressible tori. That is, we can assume that J is not a satellite knot. By Thurston’s trichotomy for knots in
$S^3\setminus J$
contains no further incompressible tori. That is, we can assume that J is not a satellite knot. By Thurston’s trichotomy for knots in
![]() $S^3$
, this implies that J is a torus knot or a hyperbolic knot [Reference ThurstonThu82]. Since
$S^3$
, this implies that J is a torus knot or a hyperbolic knot [Reference ThurstonThu82]. Since
![]() $S_{p/q}^3(K)$
is hyperbolic, it is atoroidal and irreducible. Consequently, after surgery the solid torus V must become another solid torus. However, Gabai has classified knots in a solid torus with nontrivial solid torus surgeries, showing that K is either a torus knot or a one-bridge braid in V [Reference GabaiGab89]. Moreover, since solid torus fillings on one-bridge braids only occur for integer surgery slopes, K is a cable of J unless
$S_{p/q}^3(K)$
is hyperbolic, it is atoroidal and irreducible. Consequently, after surgery the solid torus V must become another solid torus. However, Gabai has classified knots in a solid torus with nontrivial solid torus surgeries, showing that K is either a torus knot or a one-bridge braid in V [Reference GabaiGab89]. Moreover, since solid torus fillings on one-bridge braids only occur for integer surgery slopes, K is a cable of J unless
![]() $q=1$
. In either event, we have that
$q=1$
. In either event, we have that
where the slope
![]() $p/q'$
is determined by the curve bounding a disk after surgering V. Using a homological argument, one can show that
$p/q'$
is determined by the curve bounding a disk after surgering V. Using a homological argument, one can show that
![]() $q'=qw^2$
, where
$q'=qw^2$
, where
![]() $w>1$
is the winding number of K in V [Reference McA. GordonGor83, Lemma 3.3]. Since
$w>1$
is the winding number of K in V [Reference McA. GordonGor83, Lemma 3.3]. Since
![]() $S_{p/q}^3(K)$
is a hyperbolic manifold, J cannot be a torus knot. It follows that J must be a hyperbolic knot. The only remaining statement is the inequality
$S_{p/q}^3(K)$
is a hyperbolic manifold, J cannot be a torus knot. It follows that J must be a hyperbolic knot. The only remaining statement is the inequality
![]() $g(J)<g(K)$
. This follows from Schubert’s formula for the genus of a satellite knot [Reference SchubertSch53], which asserts that for a knot
$g(J)<g(K)$
. This follows from Schubert’s formula for the genus of a satellite knot [Reference SchubertSch53], which asserts that for a knot
![]() $K=P(J)$
with pattern P of winding number
$K=P(J)$
with pattern P of winding number
![]() $w\geq 0$
, there is a constant
$w\geq 0$
, there is a constant
![]() $g(P)\geq 0$
such that
$g(P)\geq 0$
such that
We obtain the necessary inequality since
![]() $w\geq 2$
.
$w\geq 2$
.
2.4 The Casson–Walker invariant
It will also be convenient to use surgery obstructions derived from the Casson–Walker invariant [Reference WalkerWal92]. For any rational homology sphere Y, this is a rational-valued invariant
![]() $\lambda (Y)\in \mathbb {Q}$
. Boyer and Lines showed that this satisfies the following surgery formula [Reference Boyer and LinesBL90]:
$\lambda (Y)\in \mathbb {Q}$
. Boyer and Lines showed that this satisfies the following surgery formula [Reference Boyer and LinesBL90]:
where
![]() $\Delta _K^{\prime \prime }(1)$
denotes the second derivative of the Alexander polynomial
$\Delta _K^{\prime \prime }(1)$
denotes the second derivative of the Alexander polynomial
![]() $\Delta _K(t)$
evaluated at
$\Delta _K(t)$
evaluated at
![]() $t=1$
. This formula immediately yields the following observation.
$t=1$
. This formula immediately yields the following observation.
Lemma 2.5 Let K and
![]() $K'$
be knots. If there is a nonzero
$K'$
be knots. If there is a nonzero
![]() $p/q\in \mathbb {Q}$
such that
$p/q\in \mathbb {Q}$
such that
![]() $S_{p/q}^3(K)\cong S_{p/q}^3(K')$
, then
$S_{p/q}^3(K)\cong S_{p/q}^3(K')$
, then
![]() $\Delta ^{\prime \prime }_{K}(1)=\Delta ^{\prime \prime }_{K'}(1)$
.
$\Delta ^{\prime \prime }_{K}(1)=\Delta ^{\prime \prime }_{K'}(1)$
.
Lemma 2.5 can be used to obstruct noncharacterizing slopes coming from cables.
Lemma 2.6 Let K and
![]() $K'$
be knots. If there is
$K'$
be knots. If there is
![]() $K"$
a nontrivial cable of
$K"$
a nontrivial cable of
![]() $K'$
and a nonzero slope
$K'$
and a nonzero slope
![]() $p/q\in \mathbb {Q}$
such that
$p/q\in \mathbb {Q}$
such that
![]() $S_{p/q}^3(K)\cong S_{p/q}^3(K")$
, then there are coprime integers
$S_{p/q}^3(K)\cong S_{p/q}^3(K")$
, then there are coprime integers
![]() $r,s$
, with
$r,s$
, with
![]() $s\geq 2$
such that
$s\geq 2$
such that
Proof Suppose that
![]() $K"$
is the
$K"$
is the
![]() $(r,s)$
-cable of
$(r,s)$
-cable of
![]() $K'$
, where
$K'$
, where
![]() $s\geq 2$
is the winding number. By the usual formula for the Alexander polynomial of a satellite knot [Reference Raymond LickorishLic97, Theorem 6.15], we have that
$s\geq 2$
is the winding number. By the usual formula for the Alexander polynomial of a satellite knot [Reference Raymond LickorishLic97, Theorem 6.15], we have that
where
![]() $T_{r,s}$
denotes the
$T_{r,s}$
denotes the
![]() $(r,s)$
-torus knot. Taking second derivatives, we obtainFootnote
1
$(r,s)$
-torus knot. Taking second derivatives, we obtainFootnote
1
Since the torus knot
![]() $T_{r,s}$
has symmetrized Alexander polynomial
$T_{r,s}$
has symmetrized Alexander polynomial
one can calculate thatFootnote 2
Combining (2.3) and (2.4) with Lemma 2.5 gives the desired statement.
We will be applying these obstructions to the knots
![]() $5_2$
and
$5_2$
and
![]() $12n242$
. These have symmetrized Alexander polynomials:
$12n242$
. These have symmetrized Alexander polynomials:
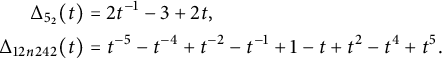 $$ \begin{align*} \Delta_{5_2}(t)&=2t^{-1}-3+2t,\\ \Delta_{12n242}(t)&=t^{-5}-t^{-4}+t^{-2}-t^{-1}+1-t +t^2-t^4+t^5. \end{align*} $$
$$ \begin{align*} \Delta_{5_2}(t)&=2t^{-1}-3+2t,\\ \Delta_{12n242}(t)&=t^{-5}-t^{-4}+t^{-2}-t^{-1}+1-t +t^2-t^4+t^5. \end{align*} $$
Hence, one finds that
2.5 An obstruction from
 $\nu ^+$
$\nu ^+$
Here, we take some input from knot Floer homology. Recall that for a knot K in
![]() $S^3$
, Ni and Wu derived a nonincreasing sequence of nonnegative integers
$S^3$
, Ni and Wu derived a nonincreasing sequence of nonnegative integers
![]() $V_0(K),V_1(K), \dots $
from the knot Floer chain complex which can be used to calculate the d-invariants of surgeries on K. For
$V_0(K),V_1(K), \dots $
from the knot Floer chain complex which can be used to calculate the d-invariants of surgeries on K. For
![]() $p/q>0$
and an appropriate identification of
$p/q>0$
and an appropriate identification of
![]() ${\mathrm {Spin}^c}(S_{p/q}^3(K))$
and
${\mathrm {Spin}^c}(S_{p/q}^3(K))$
and
![]() ${\mathrm {Spin}^c}(S_{p/q}^3(U))$
with
${\mathrm {Spin}^c}(S_{p/q}^3(U))$
with
![]() $\{0,1, \dots , p-1\}$
, we have [Reference Ni and WuNW15, Proposition 1.6]
$\{0,1, \dots , p-1\}$
, we have [Reference Ni and WuNW15, Proposition 1.6]
Hom and Wu defined the invariant
![]() $\nu ^+(K)$
to be the smallest index i for which
$\nu ^+(K)$
to be the smallest index i for which
![]() $V_i=0$
[Reference Hom and ZhongtaoHW16]. In particular, we have
$V_i=0$
[Reference Hom and ZhongtaoHW16]. In particular, we have
![]() $\nu ^+(K)=0$
if and only if
$\nu ^+(K)=0$
if and only if
![]() $V_0=0$
.
$V_0=0$
.
Lemma 2.7 Let K be a knot such that
![]() $\nu ^+(K)>0$
and
$\nu ^+(K)>0$
and
![]() $\nu ^+(mK)=0$
. Then there is no nonzero slope
$\nu ^+(mK)=0$
. Then there is no nonzero slope
![]() $p/q\in \mathbb {Q}$
such that
$p/q\in \mathbb {Q}$
such that
![]() $S_{p/q}^3(K)\cong S_{p/q}^3(mK)$
.
$S_{p/q}^3(K)\cong S_{p/q}^3(mK)$
.
Proof Since
![]() $-S_{p/q}^3(K)\cong S_{-p/q}^3(mK)$
, we can assume that
$-S_{p/q}^3(K)\cong S_{-p/q}^3(mK)$
, we can assume that
![]() $p/q>0$
. Summing the formula (2.6) over all
$p/q>0$
. Summing the formula (2.6) over all
![]() ${\mathrm {spin}^c}$
-structures on
${\mathrm {spin}^c}$
-structures on
![]() $S_{p/q}^3(mK)$
and
$S_{p/q}^3(mK)$
and
![]() $S_{p/q}^3(K)$
, we see that
$S_{p/q}^3(K)$
, we see that
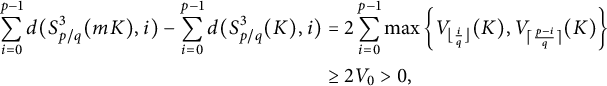 $$ \begin{align*} \sum_{i=0}^{p-1} d(S_{p/q}^3(mK),i) - \sum_{i=0}^{p-1} d(S_{p/q}^3(K),i)&=2 \sum_{i=0}^{p-1} \max\left\{V_{\lfloor\frac{i}{q}\rfloor}(K),V_{\lceil\frac{p-i}{q}\rceil}(K)\right\}\\ &\geq 2V_0>0, \end{align*} $$
$$ \begin{align*} \sum_{i=0}^{p-1} d(S_{p/q}^3(mK),i) - \sum_{i=0}^{p-1} d(S_{p/q}^3(K),i)&=2 \sum_{i=0}^{p-1} \max\left\{V_{\lfloor\frac{i}{q}\rfloor}(K),V_{\lceil\frac{p-i}{q}\rceil}(K)\right\}\\ &\geq 2V_0>0, \end{align*} $$
which implies that
![]() $S_{p/q}^3(mK)$
and
$S_{p/q}^3(mK)$
and
![]() $S_{p/q}^3(mK)$
cannot be homeomorphic.
$S_{p/q}^3(mK)$
cannot be homeomorphic.
Remark 2.8 We note that Lemma 2.7 applies to any nontrivial L-space knot (and in particular
![]() $12n242$
). For a nontrivial L-space knot, one has
$12n242$
). For a nontrivial L-space knot, one has
![]() $\nu ^+(K)=g(K)>0$
[Reference Hom and ZhongtaoHW16] and
$\nu ^+(K)=g(K)>0$
[Reference Hom and ZhongtaoHW16] and
![]() $\nu ^+(mK)=0$
[Reference GainullinGai17, Lemma 16].
$\nu ^+(mK)=0$
[Reference GainullinGai17, Lemma 16].
3 Proof of Theorem 1.1
Throughout this section, we take
![]() $K=12n242$
. Suppose that
$K=12n242$
. Suppose that
![]() $p/q\neq 0$
is a noncharacterizing slope for K satisfying
$p/q\neq 0$
is a noncharacterizing slope for K satisfying
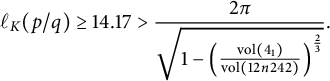 $$ \begin{align} \ell_{K}(p/q)\geq 14.17> \frac{2\pi}{\sqrt{1-\left(\frac{\mathrm{vol}(4_1)}{\mathrm{vol}(12n242)}\right)^{\frac23}}}. \end{align} $$
$$ \begin{align} \ell_{K}(p/q)\geq 14.17> \frac{2\pi}{\sqrt{1-\left(\frac{\mathrm{vol}(4_1)}{\mathrm{vol}(12n242)}\right)^{\frac23}}}. \end{align} $$
Let
![]() $K'\neq K$
be a knot in
$K'\neq K$
be a knot in
![]() $S^3$
such that
$S^3$
such that
![]() $S_{p/q}^3(K)\cong S_{p/q}^3(K')$
.
$S_{p/q}^3(K)\cong S_{p/q}^3(K')$
.
The length bound (3.1) implies that the manifold
![]() $S_{p/q}^3(K)$
is hyperbolic and, using Lemma 2.2, that
$S_{p/q}^3(K)$
is hyperbolic and, using Lemma 2.2, that
![]() $S_{p/q}^3(K)$
cannot be obtained by any surgery on the figure-eight knot
$S_{p/q}^3(K)$
cannot be obtained by any surgery on the figure-eight knot
![]() $4_1$
. By Thurston’s trichotomy for knots in
$4_1$
. By Thurston’s trichotomy for knots in
![]() $S^3$
, the knot
$S^3$
, the knot
![]() $K'$
is either a torus knot, a hyperbolic knot or a satellite knot. Since torus knots never yield a hyperbolic manifold by surgery [Reference MoserMos71], we may ignore the first possibility and restrict our attention to the latter two options.
$K'$
is either a torus knot, a hyperbolic knot or a satellite knot. Since torus knots never yield a hyperbolic manifold by surgery [Reference MoserMos71], we may ignore the first possibility and restrict our attention to the latter two options.
Claim 1 If
![]() $K'$
is a hyperbolic knot, then
$K'$
is a hyperbolic knot, then
Proof Suppose that
![]() $K'$
is a hyperbolic knot. Condition (3.1) eliminates the possibility that
$K'$
is a hyperbolic knot. Condition (3.1) eliminates the possibility that
![]() $K'$
is
$K'$
is
![]() $4_1$
. By consideration of the Casson–Walker invariant as in Lemma 2.5, we see that
$4_1$
. By consideration of the Casson–Walker invariant as in Lemma 2.5, we see that
![]() $K'$
is not
$K'$
is not
![]() $5_2$
or
$5_2$
or
![]() $m5_2$
. Using the
$m5_2$
. Using the
![]() $\nu ^+$
invariant as in Lemma 2.7, we see that
$\nu ^+$
invariant as in Lemma 2.7, we see that
![]() $K'$
is not
$K'$
is not
![]() $m12n242$
. Thus, having exhausted all the low volume knots in Theorem 2.1, we may conclude that
$m12n242$
. Thus, having exhausted all the low volume knots in Theorem 2.1, we may conclude that
![]() $\mathrm {vol}(K')>3.07$
. Thus, by Lemma 2.2, we have the bound
$\mathrm {vol}(K')>3.07$
. Thus, by Lemma 2.2, we have the bound
 $$ \begin{align*} \ell_{K'}(p/q)<\frac{2\pi}{\sqrt{1-\left(\frac{\mathrm{vol}(12n242)}{3.07}\right)^{\frac23}}}<27.34. \end{align*} $$
$$ \begin{align*} \ell_{K'}(p/q)<\frac{2\pi}{\sqrt{1-\left(\frac{\mathrm{vol}(12n242)}{3.07}\right)^{\frac23}}}<27.34. \end{align*} $$
Using Lemma 2.3, this yields the required bound.
Claim 2 If
![]() $K'$
is a satellite knot and
$K'$
is a satellite knot and
![]() $q\geq 2$
, then
$q\geq 2$
, then
Proof Suppose that
![]() $K'$
is a satellite knot and that
$K'$
is a satellite knot and that
![]() $q\geq 2$
. By (3.1), the manifold
$q\geq 2$
. By (3.1), the manifold
![]() $S_{p/q}^3(K)$
is hyperbolic and Lemma 2.4 applies to show that
$S_{p/q}^3(K)$
is hyperbolic and Lemma 2.4 applies to show that
![]() $K'$
is a cable of a hyperbolic knot J such that
$K'$
is a cable of a hyperbolic knot J such that
![]() $g(J)<g(K')$
and
$g(J)<g(K')$
and
![]() $S_{p/q'}^3(J)\cong S_{p/q}^3(K)$
for some
$S_{p/q'}^3(J)\cong S_{p/q}^3(K)$
for some
![]() $q'>q$
. By the assumption (3.1), we see that J is not
$q'>q$
. By the assumption (3.1), we see that J is not
![]() $4_1$
. Furthermore, applying the Casson–Walker invariant as in Lemma 2.6, we see that J cannot be
$4_1$
. Furthermore, applying the Casson–Walker invariant as in Lemma 2.6, we see that J cannot be
![]() $5_2$
,
$5_2$
,
![]() $m5_2$
,
$m5_2$
,
![]() $12n242$
or
$12n242$
or
![]() $m12n242$
. This is because there are no nontrivial integer solutions with
$m12n242$
. This is because there are no nontrivial integer solutions with
![]() $s\geq 2$
to the equations:
$s\geq 2$
to the equations:
and
Thus, having ruled out all the knots of small volume in Theorem 2.1, the only remaining possibility is that J must be a knot with
![]() $\mathrm {vol}(J)> 3.07$
. Thus, by Lemma 2.2, we have the bound
$\mathrm {vol}(J)> 3.07$
. Thus, by Lemma 2.2, we have the bound
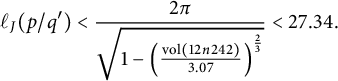 $$ \begin{align*} \ell_{J}(p/q')<\frac{2\pi}{\sqrt{1-\left(\frac{\mathrm{vol}(12n242)}{3.07}\right)^{\frac23}}}<27.34. \end{align*} $$
$$ \begin{align*} \ell_{J}(p/q')<\frac{2\pi}{\sqrt{1-\left(\frac{\mathrm{vol}(12n242)}{3.07}\right)^{\frac23}}}<27.34. \end{align*} $$
Applying Lemma 2.3 along with the inequalities
![]() $q<q'$
and
$q<q'$
and
![]() $g(J)<g(K')$
give the required bounds.
$g(J)<g(K')$
give the required bounds.
Claim 3 If
![]() $K'$
is a satellite knot and
$K'$
is a satellite knot and
![]() $p/q\geq 9$
, then
$p/q\geq 9$
, then
Proof Suppose that
![]() $K'$
is a satellite knot and
$K'$
is a satellite knot and
![]() $p/q\geq 2g(K)-1=9$
. Since K is an L-space knot, this implies that
$p/q\geq 2g(K)-1=9$
. Since K is an L-space knot, this implies that
![]() $S_{p/q}^3(K)$
is a hyperbolic L-space. By Lemma 2.4, there is a hyperbolic knot J such that
$S_{p/q}^3(K)$
is a hyperbolic L-space. By Lemma 2.4, there is a hyperbolic knot J such that
![]() $g(J)<g(K')$
and
$g(J)<g(K')$
and
![]() $S_{p/q'}^3(J)\cong S_{p/q}^3(K)$
for some
$S_{p/q'}^3(J)\cong S_{p/q}^3(K)$
for some
![]() $q'>q$
. Since
$q'>q$
. Since
![]() $\Delta _{K}^{\prime \prime }(1)\neq 0$
, [Reference Boyer and LinesBL90, Proposition 5.1] shows that J is not
$\Delta _{K}^{\prime \prime }(1)\neq 0$
, [Reference Boyer and LinesBL90, Proposition 5.1] shows that J is not
![]() $12n242$
. Furthermore, since
$12n242$
. Furthermore, since
![]() $S_{p/q'}^3(J)$
is an L-space and none of
$S_{p/q'}^3(J)$
is an L-space and none of
![]() $4_1, 5_2, m5_2$
or
$4_1, 5_2, m5_2$
or
![]() $m12n242$
are L-space knots, Theorem 2.1 allows us to conclude that
$m12n242$
are L-space knots, Theorem 2.1 allows us to conclude that
![]() $\mathrm {vol}(J)>3.07$
. Thus, as before, we arrive at the bounds
$\mathrm {vol}(J)>3.07$
. Thus, as before, we arrive at the bounds
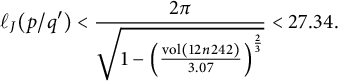 $$ \begin{align*} \ell_{J}(p/q')<\frac{2\pi}{\sqrt{1-\left(\frac{\mathrm{vol}(12n242)}{3.07}\right)^{\frac23}}}<27.34. \end{align*} $$
$$ \begin{align*} \ell_{J}(p/q')<\frac{2\pi}{\sqrt{1-\left(\frac{\mathrm{vol}(12n242)}{3.07}\right)^{\frac23}}}<27.34. \end{align*} $$
Applying Lemma 2.3(b) and
![]() $g(J)<g(K')$
gives the required bounds.
$g(J)<g(K')$
gives the required bounds.
We now convert these statements into results on characterizing slopes. The bound
![]() $q\geq 49$
is straight forward.
$q\geq 49$
is straight forward.
Claim 4 The slope
![]() $p/q$
is a characterizing slope for K whenever
$p/q$
is a characterizing slope for K whenever
![]() $q\geq 49$
.
$q\geq 49$
.
Proof Together Claims 1 and 2 show that
![]() $p/q$
is a characterizing slope for K whenever
$p/q$
is a characterizing slope for K whenever
![]() $\ell _{K}(p/q)\geq 14.17$
and
$\ell _{K}(p/q)\geq 14.17$
and
![]() $q\geq 49$
. However, Lemma 2.3(a) shows that
$q\geq 49$
. However, Lemma 2.3(a) shows that
![]() $\ell _{K}(p/q)\geq 14.17$
is automatically satisfied whenever
$\ell _{K}(p/q)\geq 14.17$
is automatically satisfied whenever
![]() $q\geq 49$
.
$q\geq 49$
.
In order to obtain the other conditions on characterizing slopes, we need to invoke results linking the genera of K and
![]() $K'$
.
$K'$
.
Claim 5 The slope
![]() $p/q$
is a characterizing slope for K whenever
$p/q$
is a characterizing slope for K whenever
![]() $p\geq \max \{24q, 441\}$
.
$p\geq \max \{24q, 441\}$
.
Proof Since
![]() $S_{18}^3(K)$
is a lens space, it bounds a sharp 4-manifold [Reference Ozsváth and SzabóOS03].Footnote
3
Thus, [Reference McCoyMcC21, Theorem 1.2] applies to show that
$S_{18}^3(K)$
is a lens space, it bounds a sharp 4-manifold [Reference Ozsváth and SzabóOS03].Footnote
3
Thus, [Reference McCoyMcC21, Theorem 1.2] applies to show that
![]() $S_{p/q}^3(K)$
bounds a sharp 4-manifold for all
$S_{p/q}^3(K)$
bounds a sharp 4-manifold for all
![]() $p/q\geq 18$
. In particular, we may apply [Reference McCoyMcC21, Theorem 1.1] to show that if
$p/q\geq 18$
. In particular, we may apply [Reference McCoyMcC21, Theorem 1.1] to show that if
![]() $p/q\geq 4g(K)+4=24$
, then
$p/q\geq 4g(K)+4=24$
, then
![]() $g(K')=g(K)=5$
. Thus, Claims 1 and 3 imply that
$g(K')=g(K)=5$
. Thus, Claims 1 and 3 imply that
![]() $p/q$
is a characterizing slope for K whenever the conditions
$p/q$
is a characterizing slope for K whenever the conditions
![]() $p\geq 24q$
,
$p\geq 24q$
,
![]() $p\geq 49(2g(K)-1)=441$
and
$p\geq 49(2g(K)-1)=441$
and
![]() $\ell _{K}(p/q)\geq 14.17$
are all satisfied. Lemma 2.3(b) shows that the bound
$\ell _{K}(p/q)\geq 14.17$
are all satisfied. Lemma 2.3(b) shows that the bound
![]() $\ell _{K}(p/q)\geq 14.17$
is redundant, being implied by
$\ell _{K}(p/q)\geq 14.17$
is redundant, being implied by
![]() $p\geq 441$
. Thus, we have a characterizing slope for K if
$p\geq 441$
. Thus, we have a characterizing slope for K if
![]() $p\geq 24q$
and
$p\geq 24q$
and
![]() $p\geq 441$
.
$p\geq 441$
.
Claim 6 The slope
![]() $p/q$
is a characterizing slope for K whenever
$p/q$
is a characterizing slope for K whenever
Proof By [Reference McCoyMcC20, Theorem 1.8(ii)], we see that if
![]() $q\geq 2$
and
$q\geq 2$
and
![]() $p\leq \min \{2q-12-4q^2, -10q\}$
, then
$p\leq \min \{2q-12-4q^2, -10q\}$
, then
![]() $g(K')=g(K)=5$
. Thus, Claims 1 and 2 imply that
$g(K')=g(K)=5$
. Thus, Claims 1 and 2 imply that
![]() $p/q$
is a characterizing slope for K if the conditions
$p/q$
is a characterizing slope for K if the conditions
![]() $q\geq 2$
,
$q\geq 2$
,
![]() $p\leq -\max \{12+4q^2-2q, 10q\}$
,
$p\leq -\max \{12+4q^2-2q, 10q\}$
,
![]() $p\leq -441$
, and
$p\leq -441$
, and
![]() $\ell _{K}(p/q)\geq 14.17$
are all satisfied. Since
$\ell _{K}(p/q)\geq 14.17$
are all satisfied. Since
![]() $12+4q^2-2q> 10q$
for all q and the condition
$12+4q^2-2q> 10q$
for all q and the condition
![]() $p\leq -441$
implies
$p\leq -441$
implies
![]() $\ell _{K}(p/q)\geq 14.17$
, we see that the conditions
$\ell _{K}(p/q)\geq 14.17$
, we see that the conditions
![]() $p\leq -12+4q^2-2q$
,
$p\leq -12+4q^2-2q$
,
![]() $q\geq 2$
, and
$q\geq 2$
, and
![]() $p\leq -441$
are sufficient to imply that
$p\leq -441$
are sufficient to imply that
![]() $p/q$
is a characterizing slope for K.
$p/q$
is a characterizing slope for K.
This completes the proof of all bounds in Theorem 1.1.
4 Constructing some noncharacterizing slopes
In this section, we construct some examples of hyperbolic knots with noncharacterizing slopes with arbitrarily large denominator. Brakes used an essentially identical construction to exhibit examples noncharacterizing slopes on satellite knots [Reference BrakesBra80]. Let
![]() $L=C'\cup K'$
be a link with two unknotted components and linking number
$L=C'\cup K'$
be a link with two unknotted components and linking number
![]() $\operatorname {\mathrm {link}}(C',K')=\omega $
. Let Y be the manifold obtained by performing
$\operatorname {\mathrm {link}}(C',K')=\omega $
. Let Y be the manifold obtained by performing
![]() $1/n$
-surgery on both components on L for some nonzero integer
$1/n$
-surgery on both components on L for some nonzero integer
![]() $n\in \mathbb {Z}$
. Since
$n\in \mathbb {Z}$
. Since
![]() $C'$
and
$C'$
and
![]() $K'$
are both unknotted, performing
$K'$
are both unknotted, performing
![]() $1/n$
surgery on one or other of them individually again results in
$1/n$
surgery on one or other of them individually again results in
![]() $S^3$
. Performing such a surgery shows that Y arises by
$S^3$
. Performing such a surgery shows that Y arises by
![]() $(n\omega ^2+ \frac {1}{n})$
-surgery on the knots K and C, where K is the image of
$(n\omega ^2+ \frac {1}{n})$
-surgery on the knots K and C, where K is the image of
![]() $K'$
in the copy of
$K'$
in the copy of
![]() $S^3$
obtained by surgering
$S^3$
obtained by surgering
![]() $C'$
and C is the image of
$C'$
and C is the image of
![]() $C'$
after surgering
$C'$
after surgering
![]() $K'$
. If one chose L wisely, then the knots K and C will be distinct and thus the slope
$K'$
. If one chose L wisely, then the knots K and C will be distinct and thus the slope
![]() $n\omega ^2+ \frac {1}{n}$
will be noncharacterizing for K and C.
$n\omega ^2+ \frac {1}{n}$
will be noncharacterizing for K and C.
Using this idea, we can prove the following.
Proposition 4.1 Let K be a knot with
![]() $g(K)\geq 2$
which can be unknotted by adding q positive full twists along two oppositely oriented strands. Then
$g(K)\geq 2$
which can be unknotted by adding q positive full twists along two oppositely oriented strands. Then
![]() $\frac {1}{q}$
is a noncharacterizing slope for K.
$\frac {1}{q}$
is a noncharacterizing slope for K.
Proof The hypothesis on unknotting implies that we can take a link
![]() $L=C'\cup K'$
with unknotted components such that (a) K can be obtained from
$L=C'\cup K'$
with unknotted components such that (a) K can be obtained from
![]() $K'$
by performing
$K'$
by performing
![]() $1/q$
-surgery on
$1/q$
-surgery on
![]() $C'$
and (b)
$C'$
and (b)
![]() $C'$
bounds a disk D that intersects
$C'$
bounds a disk D that intersects
![]() $K'$
in two oppositely oriented points. If we take the disk D and add a tube that follows an arc of
$K'$
in two oppositely oriented points. If we take the disk D and add a tube that follows an arc of
![]() $K'$
, we obtain an embedded genus one surface
$K'$
, we obtain an embedded genus one surface
![]() $\Sigma $
with boundary
$\Sigma $
with boundary
![]() $C'$
which is disjoint from
$C'$
which is disjoint from
![]() $K'$
. Since
$K'$
. Since
![]() $\Sigma $
is disjoint from
$\Sigma $
is disjoint from
![]() $K'$
, it is preserved under surgery on
$K'$
, it is preserved under surgery on
![]() $K'$
and hence shows that the knot C obtained by performing
$K'$
and hence shows that the knot C obtained by performing
![]() $1/q$
surgery on
$1/q$
surgery on
![]() $K'$
has genus at most one. Since K is assumed to have genus at least two, this implies that C is not isotopic to K and hence that
$K'$
has genus at most one. Since K is assumed to have genus at least two, this implies that C is not isotopic to K and hence that
![]() $1/q$
is a noncharacterizing slope for K.
$1/q$
is a noncharacterizing slope for K.
Example 4.2 Using the preceding proposition, we can show that for every
![]() $q\geq 1$
, there is a hyperbolic two-bridge knot
$q\geq 1$
, there is a hyperbolic two-bridge knot
![]() $K_q$
for which
$K_q$
for which
![]() $\frac {1}{q}$
is a noncharacterizing slope. Figure 2 depicts a two-bridge knot
$\frac {1}{q}$
is a noncharacterizing slope. Figure 2 depicts a two-bridge knot
![]() $K_q$
of genus two that can be unknotted by adding q positive full twists along two oppositely oriented strands. The genus of
$K_q$
of genus two that can be unknotted by adding q positive full twists along two oppositely oriented strands. The genus of
![]() $K_q$
can be easily verified, since Seifert’s algorithm always yields a minimal genus Seifert surface when applied to an alternating diagram [Reference CrowellCro59, Reference MurasugiMur58]. Thus, Proposition 4.1 applies to
$K_q$
can be easily verified, since Seifert’s algorithm always yields a minimal genus Seifert surface when applied to an alternating diagram [Reference CrowellCro59, Reference MurasugiMur58]. Thus, Proposition 4.1 applies to
![]() $K_q$
. Figure 3 shows how one can obtain a knot
$K_q$
. Figure 3 shows how one can obtain a knot
![]() $C_q$
such that
$C_q$
such that
![]() $S_{\frac {1}{q}}^3(C_q)\cong S_{\frac {1}{q}}^3(K_q)$
.
$S_{\frac {1}{q}}^3(C_q)\cong S_{\frac {1}{q}}^3(K_q)$
.
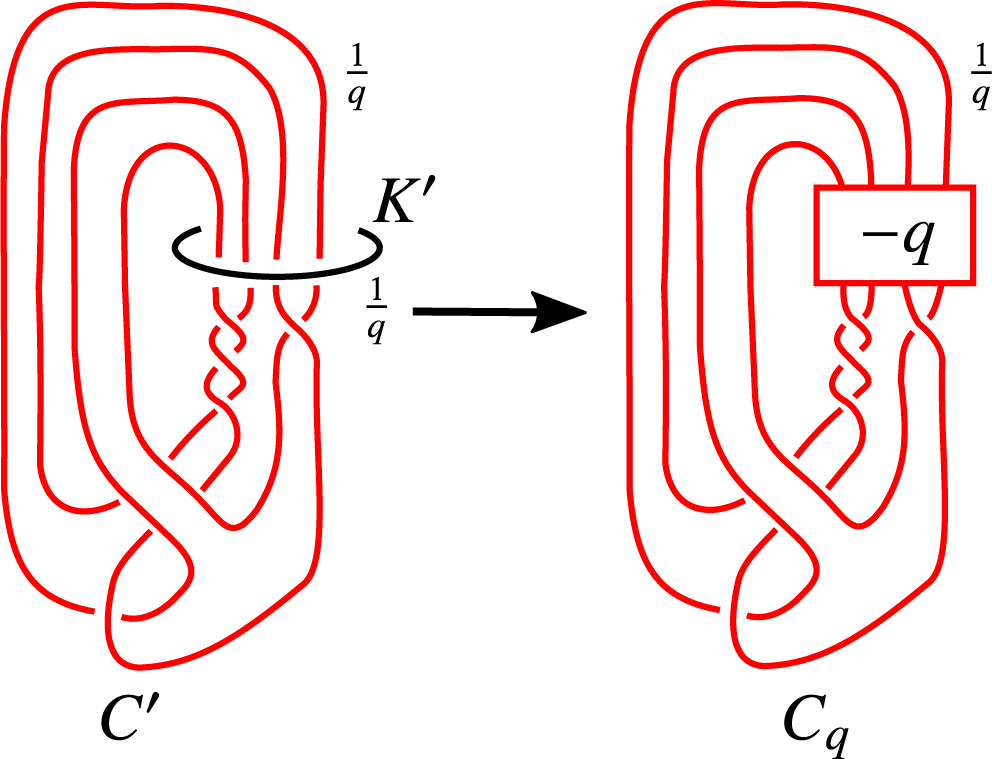
Figure 3 The link
![]() $K'\cup C'$
isotoped so that
$K'\cup C'$
isotoped so that
![]() $K'$
appears as a round unknot. A knot
$K'$
appears as a round unknot. A knot
![]() $C_q$
such that
$C_q$
such that
![]() $S_{\frac {1}{q}}^3(C_q)\cong S_{\frac {1}{q}}^3(K_q)$
is, thus, obtained by adding q negative full twists along
$S_{\frac {1}{q}}^3(C_q)\cong S_{\frac {1}{q}}^3(K_q)$
is, thus, obtained by adding q negative full twists along
![]() $C'$
.
$C'$
.
We also note that sufficiently complicated knots with unknotting number one must always have an noncharacterizing slope. Since every slope is characterizing for the trefoil and the figure-eight knot [Reference Ozsváth and SzabóOS19], we see that the condition on the genus cannot be relaxed.
Corollary 4.3 Let K be a knot with
![]() $g(K)\geq 2$
and
$g(K)\geq 2$
and
![]() $u(K)=1$
.
$u(K)=1$
.
-
• If K can be unknotted by changing a positive crossing, then
 $+1$
is noncharacterizing for K.
$+1$
is noncharacterizing for K. -
• If K can be unknotted by changing a negative crossing, then
 $-1$
is noncharacterizing for K.
$-1$
is noncharacterizing for K.
A Calculating
 $\Delta _{T_{r,s}}^{\prime \prime }(1)$
$\Delta _{T_{r,s}}^{\prime \prime }(1)$
We conclude with a derivation of (2.4). It will be convenient to define, for any positive integer k, the function
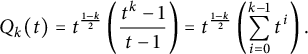 $$\begin{align*}Q_k(t)=t^{\frac{1-k}{2}}\left(\frac{t^k-1}{t-1}\right)=t^{\frac{1-k}{2}}\left(\sum_{i=0}^{k-1} t^i\right).\end{align*}$$
$$\begin{align*}Q_k(t)=t^{\frac{1-k}{2}}\left(\frac{t^k-1}{t-1}\right)=t^{\frac{1-k}{2}}\left(\sum_{i=0}^{k-1} t^i\right).\end{align*}$$
Using these, we can write the Alexander polynomial of a torus knot in the form:
Since
![]() $Q_k(t)=Q_{k}(t^{-1})$
, we have that
$Q_k(t)=Q_{k}(t^{-1})$
, we have that
Furthermore, we calculate that
and
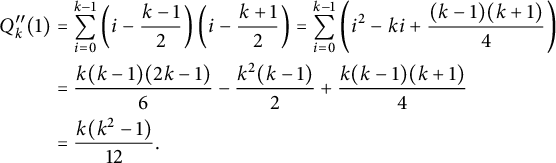 $$ \begin{align*} Q_k^{\prime\prime}(1)&=\sum_{i=0}^{k-1} \left(i - \frac{k-1}{2}\right)\left(i - \frac{k+1}{2}\right)= \sum_{i=0}^{k-1} \left(i^2 -ki + \frac{(k-1)(k+1)}{4}\right)\\ &=\frac{k(k-1)(2k-1)}{6}- \frac{k^2(k-1)}{2}+ \frac{k(k-1)(k+1)}{4}\\ &=\frac{k(k^2-1)}{12}. \end{align*} $$
$$ \begin{align*} Q_k^{\prime\prime}(1)&=\sum_{i=0}^{k-1} \left(i - \frac{k-1}{2}\right)\left(i - \frac{k+1}{2}\right)= \sum_{i=0}^{k-1} \left(i^2 -ki + \frac{(k-1)(k+1)}{4}\right)\\ &=\frac{k(k-1)(2k-1)}{6}- \frac{k^2(k-1)}{2}+ \frac{k(k-1)(k+1)}{4}\\ &=\frac{k(k^2-1)}{12}. \end{align*} $$
These identities allow us to calculate
![]() $\Delta _{T_{r,s}}^{\prime \prime }(1)$
implicitly. Differentiating the identity
$\Delta _{T_{r,s}}^{\prime \prime }(1)$
implicitly. Differentiating the identity
twice and evaluating at
![]() $t=1$
, we obtain
$t=1$
, we obtain
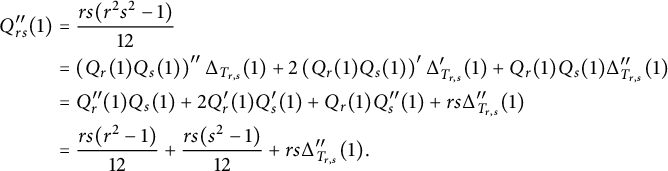 $$ \begin{align*} Q_{rs}^{\prime\prime}(1)&=\frac{rs(r^2s^2-1)}{12}\\ &= \left(Q_{r}(1)Q_{s}(1)\right)"\Delta_{T_{r,s}}(1)+2\left(Q_{r}(1)Q_{s}(1)\right)'\Delta_{T_{r,s}}'(1)+ Q_{r}(1)Q_{s}(1)\Delta_{T_{r,s}}^{\prime\prime}(1)\\ &=Q_{r}^{\prime\prime}(1)Q_{s}(1)+2Q_{r}^{\prime}(1)Q_{s}^{\prime}(1)+ Q_{r}(1)Q_{s}^{\prime\prime}(1)+rs\Delta_{T_{r,s}}^{\prime\prime}(1)\\ &=\frac{rs(r^2-1)}{12}+\frac{rs(s^2-1)}{12}+rs\Delta_{T_{r,s}}^{\prime\prime}(1). \end{align*} $$
$$ \begin{align*} Q_{rs}^{\prime\prime}(1)&=\frac{rs(r^2s^2-1)}{12}\\ &= \left(Q_{r}(1)Q_{s}(1)\right)"\Delta_{T_{r,s}}(1)+2\left(Q_{r}(1)Q_{s}(1)\right)'\Delta_{T_{r,s}}'(1)+ Q_{r}(1)Q_{s}(1)\Delta_{T_{r,s}}^{\prime\prime}(1)\\ &=Q_{r}^{\prime\prime}(1)Q_{s}(1)+2Q_{r}^{\prime}(1)Q_{s}^{\prime}(1)+ Q_{r}(1)Q_{s}^{\prime\prime}(1)+rs\Delta_{T_{r,s}}^{\prime\prime}(1)\\ &=\frac{rs(r^2-1)}{12}+\frac{rs(s^2-1)}{12}+rs\Delta_{T_{r,s}}^{\prime\prime}(1). \end{align*} $$
From this, one rearranges to obtain the desired formula:
Acknowledgment
The author would like to thank Steve Boyer and Patricia Sorya for interesting conversations. He is also grateful to an anonymous referee for their comments, in particular, for pointing out the work of Brakes [Reference BrakesBra80].