Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T12:43:47.088Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterizations of Operator Birkhoff–James Orthogonality

Published online by Cambridge University Press:  20 November 2018

Mohammad Sal Moslehian  and
Ali Zamani
Mohammad Sal Moslehian
Affiliation:
Department of Pure Mathematics, Ferdowsi University of Mashhad, P.O. Box 1159, Mashhad 91775, Iran e-mail: [email protected]
Ali Zamani
Affiliation:
Department of Mathematics, Farhangian University, Iran e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

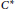In this paper, we obtain some characterizations of the (strong) Birkhoff–James orthogonality for elements of Hilbert ${{C}^{*}}$-modules and certain elements of $\mathbb{B}\left( H \right)$. Moreover, we obtain a kind of Pythagorean relation for bounded linear operators. In addition, for 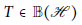$T\in \mathbb{B}(H)$ we prove that if the norm attaining set ${{\mathbb{M}}_{T}}$ is a unit sphere of some finite dimensional subspace 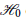${{H}_{0}}$ of 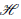$H$ and 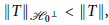$||T|{{|}_{{{H}_{0}}\bot }}\,<\,\,||T||$, then for every 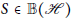$S\in \mathbb{B}(H)$, 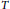$T$ is the strong Birkhoff–James orthogonal to $S$ if and only if there exists a unit vector 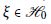$\xi \in {{H}_{0}}$ such that $||T||\xi =\,|T|\xi $ and 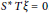${{S}^{*}}T\xi =0$. Finally, we introduce a new type of approximate orthogonality and investigate this notion in the setting of inner product 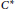${{C}^{*}}$-modules.

Keywords

46L0546L0846B20Hilbert C*-moduleBirkhoÒ–James orthogonalitystrong BirkhoÒ–James orthogonalityapproximate orthogonality
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 4 , 01 December 2017 , pp. 816 - 829
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Aldaz, J. M., S. Barza, M. Fujii, and Moslehian, M. S., Advances in operator Cauchy-Schwarz inequalities and their reverses. Ann. Funct. Anal. 6(2015), no. 3, 275–295. http://dx.doi.org/1 0.1 5352/afa/O6-3-2O Google Scholar
[2] Arambasic, Lj. and R. Rajic, A strong version of the Birkhoff-–James orthogonality in Hilbert C*-modules. Ann. Funct. Anal. 5(2014), no. 1, 109–120. http://dx.doi.org/10.15352/afa/1391614575 Google Scholar
[3] Arambasic, Lj., On three concepts of orthogonality in Hilbert C* -modules. Linear Multilinear Algebra 63(2015), no. 7, 1485–1500. http://dx.doi.org/10.1080/03081 087.201 4.947983 Google Scholar
[4] Bhatia, R. and P. Semrl, Orthogonality of matrices and some distance problems. Linear Algebra Appl. 287(1999), no. 1–3, 77-85. http://dx.doi.org/10.101 6/S0024-3795(98)10134-9 Google Scholar
[5] Bhattacharyya, T. and P. Grover, Characterization of Birkhoff-–James orthogonality. J. Math. Anal. Appl. 407(2013), no. 2, 350–358. http://dx.doi.org/10.101 6/j.jmaa.2O13.05.022 Google Scholar
[6] Birkhoff, G., Orthogonality in linear metric spaces. Duke Math. J. 1(1935), no. 2,169-172. http://dx.doi.org/10.1215/S0012-7094-35-00115-6 Google Scholar
[7] Chmieliiiski, J., On an e-Birkhoff orthogonality. J. Inequal. Pure Appl. Math. 6(2005), no. 3, Art. 79.Google Scholar
[8] Chmieliiiski, J., Linear mappings approximately preserving orthogonality. J. Math. Anal. Appl. 304(2005), 158-169. http://dx.doi.org/10.101 6/j.jmaa.2004.09.011 Google Scholar
[9] Chmieliiiski, J., Orthogonality equation with two unknown functions. Aequationes Math. 90(2016), no. 1, 11–23. http://dx.doi.org/10.1007/s00010-01 5-0359-x Google Scholar
[10] Diogo, C., Algebraic properties of the set of operators with 0 in the closure of the numerical range. Oper. Matrices 9(2015), no. 1, 83–93. http://dx.doi.org/10.71 53/oam-09-04 Google Scholar
[11] Dixmier, J., C* -Algebras. North-Holland, Amsterdam, 1981.Google Scholar
[12] Frank, M., Mishchenko, A. S., and Pavlov, A. A., Orthogonality-preserving, C*-conformal and conformal module mappings on Hilbert C*-modules. J. Funct. Anal. 260(2011), no. 2, 327–339. http://dx.doi.org/1 0.101 6/j.jfa.2O10.10.009 Google Scholar
[13] Ghosh, P., D. Sain and K. Paul, Orthogonality of bounded linear operators. Linear Algebra Appl. 500(2016), 43–51. http://dx.doi.org/10.1016/jJaa.2016.03.009 Google Scholar
[14] Grover, P., Orthogonality of matrices in the Ky Fan k-norms. Linear Multilinear Algebra 65(2017), no. 3, 496–509. http://dx.doi.org/10.1080/03081087.201 6.11 9311 8 Google Scholar
[15] Ilisevic, D. and A. Turnsek, Approximately orthogonality preserving mappings on C* -modules. J. Math. Anal. Appl. 341(2008), no. ,1 298–308. http://dx.doi.org/10.1016/j.jmaa.2007.10.028 Google Scholar
[16] James, R. C., Orthogonality in normed linear spaces. Duke Math. J. 12(1945), 291–302. http://dx.doi.org/1 0.121 5/S001 2-7094-45-01223-3 Google Scholar
[17] Lance, E. C., Hilbert C* -modules. A toolkit for operator algebraists. London Mathematical Society Lecture Note Series, 210, Cambridge University Press, Cambridge, 1995. http://dx.doi.org/1 0.101 7/CBO9780511 526206 Google Scholar
[18] Leung, C.-W., C.-K. Ng, and N.-C. Wong, Linear orthogonality preservers of Hilbert C*-modules. J. Operator Theory 71(2014), no. 2, 571–584. http://dx.doi.org/10.7900/jot.2012ju112.1966 Google Scholar
[19] Mojskerc, B. and A. Turnsek, Mappings approximately preserving orthogonality in normed spaces. Nonlinear Anal. 73(2010), no. 12, 3821–3831. http://dx.doi.org/10.1016/j.na.2O10.08.007 Google Scholar
[20] Murphy, G. J., C*-Algebras and operator theory. Academic Press, Boston, MA, 1990. Google Scholar
[21] Paul, K., D. Sain, and P. Ghosh, Birkhoff-–fames orthogonality and smoothness of bounded linear operators. Linear Algebra Appl. 506(2016), 551–563. http://dx.doi.org/10.1016/j.laa.2O16.06.024 Google Scholar
[22] Sain, D., K. Paul, and S. Hait, Operator norm attainment and Birkhoff-–James orthogonality. Linear Algebra Appl. 476(2015), 85–97. http://dx.doi.org/10.1016/j.laa.2015.03.002 Google Scholar
[23] Wojcik, P., Norm-parallelism in classical M-ideals. Indag. Math., to appear. http://dx.doi.org/1 0.101 6/j.indag.2O1 6.07.001 Google Scholar
[24] Zamani, A. and Moslehian, M. S., Exact and approximate operator parallelism. Canad. Math. Bull. 58(2015), no. 1, 207–224. http://dx.doi.org/10.4153/CMB-2014-02 9-4 Google Scholar
[25] Zamani, A., Moslehian, M. S., and M. Frank, Angle preserving mappings. Z. Anal. Anwend. 34(2015), no. 4, 485–500. http://dx.doi.org/! 0.41 71/ZAA/1 551 Google Scholar