Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T17:37:55.373Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterizations of Axiomatic Categories of Models Canonically Isomorphic to (Quasi-)Varieties

Published online by Cambridge University Press:  20 November 2018

Michel Hébert
Michel Hébert*
Affiliation:
Département de Mathématiques, Université LavalQuebec, P.Q. Canada G1K 7P4 Department of Mathematics, Mcgill UniversityMontreal, P.Q., Canada H3A 2K6
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 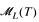be the category of all homomorphisms (i.e. functions preserving satisfaction of atomic formulas) between models of a set of sentences T in a finitary first-order language L. Functors between two such categories are said to be canonical if they commute with the forgetful functors. The following properties are characterized syntactically and also in terms of closure of 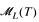for some algebraic constructions (involving products, equalizers, factorizations and kernel pairs): There is a canonical isomorphism from 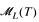to a variety (resp. quasivariety) in a finitary expansion of L which assigns to a model its (unique) expansion. This solves a problem of H. Volger.

In the case of a purely algebraic language, the properties are equivalent to:“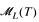 is canonically isomorphic to a finitary variety (resp. quasivariety)” and, for the variety case, to “the forgetful functor of 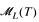is monadic (tripleable)”.

Keywords

Categories of modelspreservation theoremvarietiesmonadicity03C6008C1018C15
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 31 , Issue 3 , 01 September 1988 , pp. 287 - 300
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Burris, S., Remarks on reducts of varieties, in Universal Algebra, Coll. Math. Soc. J. Bolyai (Esztergom 1977), pp. 161–168.Google Scholar
2. Chang, C. C., Keisler, H. J., Model Theory (North-Holland, Amsterdam, 1977).Google Scholar
3. Eklof, P. C., Ultraproducts for algebraists, in Handbook of Mathematical Logic (North-Holland, Amsterdam, 1977).Google Scholar
4. Gratzer, G., Universal Algebra (Springer-Verlag, New-York 1979).Google Scholar
5. Hatcher, W. S., Whitney, S., Characterizing categories of algebras, Algebra Universalis, 19 (1984), pp. 231–242.Google Scholar
6. Hébert, M., Sur le rang et la définissabilité des opérations implicites dans les classes d'algèbres, manuscript.Google Scholar
7. Herrera, J., Les théories convexes de Horn, C.R. Acad. Se. Paris Série A, 287 (1978), pp. 593–594.Google Scholar
8. Hodges, W., Functorial uniform reducibility, Fund. Math. 108 (1980), pp. 77–81.Google Scholar
9. Isbell, J. R., Subobjects, adequacy, completeness and categories of algebras, Rozprawy Mat. 36 (1964), pp. 3–33.Google Scholar
10. Lawvere, F. W., Functorial semantics of algebraic theories, Proc. Nat. Acad. Sci. U.S.A 50 (1963), pp. 864–872.Google Scholar
11. Linton, F. E. J., Some aspects of equational categories, in Proceedings of the Conference of Categorical Algebra (La Jolla 1965) (Springer-Verlag, New-York, 1966).Google Scholar
12. MacLane, S., Categories for the Working Mathematician (Springer-Verlag, New-York, 1971).Google Scholar
13. Rabin, M. O., Classes of models and sets of sentences with the intersection property, Ann. Sci. Univ. Clermont 7 (1962), pp. 39–53.Google Scholar
14. Richter, M., Limites in Kategorien von Relationalsystemen, Z. Math. Logik Grundlagen Math. 17(1971), pp. 75–90.Google Scholar
15. Volger, H., Preservation theorems for limits of structures and global sections of sheaves of structures, Math. Z. 166 (1979), pp. 27–53.Google Scholar