Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T11:38:39.002Z Has data issue: false hasContentIssue false
  • English
  • Français

A Characterization of Varieties with a Difference Term, II: Neutral = Meet Semi-Distributive

Published online by Cambridge University Press:  20 November 2018

Paolo Lipparini
Paolo Lipparini*
Affiliation:
Dipartimento di Matematica II Università di Roma (Tor Vergata) Viale della Ricerca ascientifica I-00133 Rome Italy, e-mail: [email protected] , [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

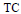We provide more characterizations of varieties with a weak difference term and of neutral varieties. We prove that a variety has a (weak) difference term (is neutral) with respect to the $\text{TC}$-commutator iff it has a (weak) difference term (is neutral) with respect to the linear commutator. We show that a variety 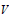$V$ is congruence meet semi-distributive iff 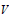$V$ is neutral, iff 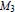${{M}_{3}}$ is not a sublattice of Con 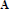$\mathbf{A}$, for 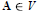$\mathbf{A}\in V$, iff there is a positive integer $n$ such that 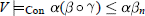$V{{\vDash }_{Con}}\alpha (\beta \,o\,\gamma )\le \alpha {{\beta }_{n}}$.

Keywords

08B0508B99
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 41 , Issue 3 , 01 September 1998 , pp. 318 - 327
Copyright
Copyright © Canadian Mathematical Society 1998

References

[BS] Burris, S., Sankappanavar, H. P., A course in universal algebra. Springer, New York, 1981.Google Scholar
[Cz] Czédli, G., A characterization of congruence semi-distributivity. In:UniversalAlgebra and Lattice Theory, Lecture Notes in Math. 1004(1983).Google Scholar
[He] Herrmann, C., Affine algebras in congruence modular varieties. Acta Sci. Math. (Szeged) 41 (1979), 119–125.Google Scholar
[HMK] Hobby, D., McKenzie, R., The structure of finite algebras. Contemp. Math. 76 (1988).Google Scholar
[Jo] Jonsson, B., Congruence Varieties. Algebra Universalis 10 (1980), 355–394.Google Scholar
[Ke] Kearnes, K. A., Commutator theory with a difference term. J.Algebra 177 (1995), 926–960.Google Scholar
[KS] Kearnes, K., Szendrei, A., The Relationship Between Two Commutators. Internat. J. Algebra Comput. (to appear).Google Scholar
[Lp1] Lipparini, P., A characterization of varieties with a difference term. Canad. Math. Bull. (3) 39 (1996), 308–315.Google Scholar
[Lp2] Lipparini, P., Difference terms and commutators. Manuscript.Google Scholar
[Lp3] Lipparini, P., n-permutable varieties satisfy non trivial congruence identities. Algebra Universalis 33 (1995), 159–168.Google Scholar
[Lp4] Lipparini, P., Commutator Theory without join-distributivity. Trans. Amer.Math. Soc. 346 (1994), 177–202.Google Scholar
[MKNT] McKenzie, R., McNulty, G. and Taylor, W., Algebras, Lattices, Varieties. Wadsworth & Brooks/Cole Mathematics Series 1, Monterey, 1987.Google Scholar
[Qu] Quackenbush, R., Quasi-affine algebras. Algebra Universalis 20 (1985), 318–327.Google Scholar
[Ta] Taylor, W., Characterizing Mal’cev conditions. Algebra Universalis 3 (1973), 351–397.Google Scholar