No CrossRef data available.
Article contents
A characterization of the existence of zeros for operators with Lipschitzian derivative and closed range
Part of:
Nonlinear functional analysis
Measures, integration, derivative, holomorphy
Equations and inequalities involving nonlinear operators
Published online by Cambridge University Press: 08 January 2025
Abstract
Let H be a real Hilbert space and 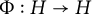 $\Phi :H\to H$ be a
$\Phi :H\to H$ be a  $C^1$ operator with Lipschitzian derivative and closed range. We prove that
$C^1$ operator with Lipschitzian derivative and closed range. We prove that 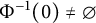 $\Phi ^{-1}(0)\neq \emptyset $ if and only if, for each
$\Phi ^{-1}(0)\neq \emptyset $ if and only if, for each  $\epsilon>0$, there exist a convex set
$\epsilon>0$, there exist a convex set 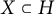 $X\subset H$ and a convex function
$X\subset H$ and a convex function 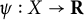 $\psi :X\to \mathbf {R}$ such that
$\psi :X\to \mathbf {R}$ such that  $\sup _{x\in X}(\|x\|^2+\psi (x))-\inf _{x\in X}(\|x\|^2+\psi (x))<\epsilon $ and
$\sup _{x\in X}(\|x\|^2+\psi (x))-\inf _{x\in X}(\|x\|^2+\psi (x))<\epsilon $ and  $0\in \overline {{\mathrm {conv}}}(\Phi (X))$.
$0\in \overline {{\mathrm {conv}}}(\Phi (X))$.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society
References
Kneser, H.,
Sur un théorème fondamental de la théorie des jeux
. C. R. Acad. Sci. Paris 234(1952), 2418–2420.Google Scholar
Zalinescu, C., Personal communication.Google Scholar
Zeidler, E., Nonlinear functional analysis and its applications. Vol. III, Springer-Verlag, New York, 1985.CrossRefGoogle Scholar



