Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T19:01:24.240Z Has data issue: false hasContentIssue false
  • English
  • Français

A Characterization of Ideals of C* -Algebras

Published online by Cambridge University Press:  20 November 2018

Masaharu Kusuda
Masaharu Kusuda*
Affiliation:
Department of Applied Mathematics Faculty of Engineering Science Osaka University Toyonaka, Osaka 560 Japan.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A be a C*-algebra and let I be a C*-subalgebra of A. Denote by 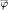an extension of a state φ of B to a state of A. It is shown that I is an ideal of A if and only if there exists a homomorphism Q from A** onto I** such that Q is the identity map on I** and 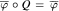for every state φ on I. Furthermore it is also shown that I is an essential ideal of A if and only if there exists an injective homomorphism from A into the multiplier algebra of I which is the identity map on I.

Keywords

46L3046L05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 33 , Issue 4 , 01 December 1990 , pp. 455 - 459
Copyright
Copyright © Canadian Mathematical Society 1990

References

1. Batty, C. J. K., Kusuda, M., Weak expectations in C*-dynamical systems, J. Math. Soc. Japan 40 No. 4 (1988) 662–669.Google Scholar
2. Green, P., The local structure of twisted covariance algebras, Acta Math. 140 (1978) 191–250.Google Scholar
3. M. Kusuda, Hereditary C*-subalgebras of C*-crossed products, Proc. Amer. Math. Soc. 102 No. 1 (1988) 90–94.Google Scholar
4. Kusuda, M., Unique state extension and hereditary C*-subalgebras, Math. Ann. (to appear).Google Scholar
5. Landstad, M. B., Phillips, J., Raeburn, I., Sutherland, C. E., Representations of crossed products by coactions and principal bundles, Trans. Amer. Math. Soc. 299 No. 2 (1987) 747–784.Google Scholar
6. Pedersen, G. K., C*-Algebras and their Automorphism Groups, Academic Press, London and New York, 1979.Google Scholar