Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T01:38:18.907Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterization of Eigenfunctions by Boundedness Conditions

Published online by Cambridge University Press:  20 November 2018

Ralph Howard  and
Margaret Reese
Ralph Howard
Affiliation:
Department of Mathematics University of South Carolina Columbia, South Carolina 29208
Margaret Reese
Affiliation:
Department of Mathematics Sa in t Olaf Co liege Northfield, Minnesota 55057
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

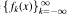Suppose is a sequence of functions on ℝn with Δfk = fk+1 (where Δ is the Laplacian) that satisfies the growth condition: |fk(x)| ≤ Mk{1 + |x|)a where a ≥ 0 and the constants have sublinear growth 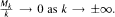Then Δf0 = —f0- This characterizes eigenfunctions f of Δ with polynomial growth in terms of the size of the powers Δkf, —∞ < k < ∞. It also generalizes results of Roe (where a = 0, Mk = M, and n = 1 ) and Strichartz (where a = 0, Mk = M for n). The analogue holds for formally self-adjoint constant coefficient linear partial differential operators on ℝn.

Keywords

42B1035B35EigenfunctionsLaplacianconstant coeffcient differential operators
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 35 , Issue 2 , 01 June 1992 , pp. 204 - 213
Copyright
Copyright © Canadian Mathematical Society 1992 

References

1. Birkoff, G. and MacLane, S., A Survey of Modern Algebra, MacMillan, New York, 1965.Google Scholar
2. Burkhill, H., Sequences characterizing the sine function, Math. Proc. Camb. Phil. Soc. 89(1981), 71–77.Google Scholar
3. Jean-Pierre Gabardo, Tempered distributions with spectral gaps, Math. Proc. Camb. Phil. Soc. 106(1989), 143–162.Google Scholar
4. Hormander, L., Linear Partial Differential Operators, Springer-Verlag, New York, 1969.Google Scholar
5. Howard, R., A note on Roe's characterization of the sine function, Proc. Amer. Math. Soc. 105(1989), 658–663.Google Scholar
6. Roe, J., A characterization of the sine function, Math. Proc. Camb. Phil. Soc. 87(1980), 69–73.Google Scholar
7. Rudin, W., Functional Analysis, McGraw-Hill, New York, 1973.Google Scholar
8. Strichartz, R. S., Characterization of eigenfunctions of the Laplacian by boundedness conditions, Trans. Amer. Math. Soc. (to appear).Google Scholar