Published online by Cambridge University Press: 20 November 2018
We investigate quantum group generalizations of various density results from Fourier analysis on compact groups. In particular, we establish the density of characters in the space of fixed points of the conjugation action on 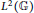 ${{L}^{2}}(\mathbb{G})$ and use this result to show the
${{L}^{2}}(\mathbb{G})$ and use this result to show the 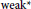 $\text{wea}{{\text{k}}^{\star }}$ density and normal density of characters in
$\text{wea}{{\text{k}}^{\star }}$ density and normal density of characters in 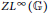 $Z{{L}^{\infty }}(\mathbb{G})$ and
$Z{{L}^{\infty }}(\mathbb{G})$ and 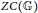 $ZC(\mathbb{G})$, respectively. As a corollary, we partially answer an open question of Woronowicz. At the level of
$ZC(\mathbb{G})$, respectively. As a corollary, we partially answer an open question of Woronowicz. At the level of 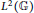 ${{L}^{1}}(\mathbb{G})$, we show that the center
${{L}^{1}}(\mathbb{G})$, we show that the center 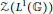 $~z({{L}^{1}}(\mathbb{G}))$ is precisely the closed linear span of the quantum characters for a large class of compact quantum groups, including arbitrary compact Kac algebras. In the latter setting, we show, in addition, that
$~z({{L}^{1}}(\mathbb{G}))$ is precisely the closed linear span of the quantum characters for a large class of compact quantum groups, including arbitrary compact Kac algebras. In the latter setting, we show, in addition, that 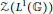 $~z({{L}^{1}}(\mathbb{G}))$ is a completely complemented
$~z({{L}^{1}}(\mathbb{G}))$ is a completely complemented 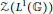 $~z({{L}^{1}}(\mathbb{G}))$-submodule of
$~z({{L}^{1}}(\mathbb{G}))$-submodule of 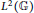 ${{L}^{2}}(\mathbb{G})$.
${{L}^{2}}(\mathbb{G})$.