Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-12T19:49:25.415Z Has data issue: false hasContentIssue false
  • English
  • Français

Certain Properties of K0-monoids Preserved by Tracial Approximation

Published online by Cambridge University Press:  20 November 2018

Qingzhai Fan
Qingzhai Fan*
Affiliation:
Department of Mathematics, Shanghai Maritime University, 1550 Haigang Ave. in New Harbor City, Shanghai 201306, China e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that the following 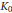${{K}_{0}}$-monoid properties of 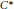${{C}^{*}}$-algebras in the class 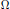$\Omega $ are inherited by simple unital 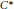${{C}^{*}}$-algebras in the class 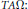$TA\Omega :$ (1) weak comparability, (2) strictly unperforated, (3) strictly cancellative.

Keywords

46L0546L8046L35C*-algebratracial approximationK0-monoid
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 2 , 01 June 2013 , pp. 337 - 343
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Blackadar, B., K-theory for operator algebra. Springer-Verlag, New York, 1986.Google Scholar
[2] Elliott, G. A., On the classification of the inductive limits of sequences of semisimple finite dimensional algebras. J. Algebra 38(1976), 29–44. http://dx.doi.org/10.1016/0021-8693(76)90242-8 Google Scholar
[3] Elliott, G. A., On the classification of C*-algebras of real rank zero. J. Reine Angew. Math. 443(1993), 179–219. http://dx.doi.org/10.1515/crll.1993.443.179 Google Scholar
[4] Elliott, G. A. and Gong, G., On the classification of C_-algebras of real rank zero, II. Ann. Math. 144(1996), 497–610. http://dx.doi.org/10.2307/2118565 Google Scholar
[5] Elliott, G. A. and Niu, Z., On tracial approximation. J. Funct. Anal. 25(2008), 396–440. http://dx.doi.org/10.1016/j.jfa.2007.08.005 Google Scholar
[6] Fan, Q. and Fang, X., Stable rank one and real rank zero for crossed product by automorphisms with the tracial Rokhlin property. Chinese Ann. Math. (Series B) 30(2009), 179–186. http://dx.doi.org/10.1007/s11401-007-0563-7 Google Scholar
[7] Fan, Q., Certain properties preserved by tracial approximation. Preprint.Google Scholar
[8] Fan, Q., Classification of certain simple C_-algebras. J. Ramanujan Math. Soc. 26(2011), 1–7. Google Scholar
[9] Fan, Q. and Fang, X., Non-simple tracial approximation. Houston J. Math., to appear.Google Scholar
[10] Lin, H., The tracial topological rank of C_-algebras. Proc. London Math. Soc. 83(2001), 199–234. http://dx.doi.org/10.1112/plms/83.1.199 Google Scholar
[11] Lin, H., An introduction to the classification of amenable C-algebras. World Sci. Publ., New Jersey–London–Singapore–Hong Kong, 2001.Google Scholar
[12] Ortega, E., Perera, F., and Rordam, M., The Corona Factorization Property and refinement monoids. arxiv:0904.0541v1.Google Scholar
[13] Wehrung, F., Injective positively ordered monoids I. J. Pure Appl. Algebra 83(1992), 43–82. http://dx.doi.org/10.1016/0022-4049(92)90104-N Google Scholar