Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T09:41:27.006Z Has data issue: false hasContentIssue false
  • English
  • Français

A Case When the Fiber of the Double Suspension is the Double Loops on Anick's Space

Published online by Cambridge University Press:  20 November 2018

Stephen D. Theriault
Stephen D. Theriault*
Affiliation:
Department of Mathematical Sciences, University of Aberdeen, Aberdeen, United Kingdom e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The fiber 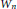${{W}_{n}}$ of the double suspension 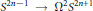${{S}^{2n-1}}\,\to \,{{\Omega }^{2}}{{S}^{2n+1}}$ is known to have a classifying space $B{{W}_{n}}$. An important conjecture linking the 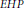$EPH$ sequence to the homotopy theory of Moore spaces is that 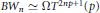$B{{W}_{n}}\,\simeq \,\Omega {{T}^{2np+1}}(p)$, where 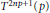${{T}^{2np+1}}(p)$ is Anick's space. This is known if 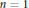$n\,=\,1$. We prove the 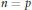$n\,=\,p$ case and establish some related properties.

Keywords

55P3555P10double suspensionAnick's space
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 53 , Issue 4 , 01 December 2010 , pp. 730 - 736
Copyright
Copyright © Canadian Mathematical Society 2010

References

[A] Anick, D., Differential algebras in topology. Research Notes in Mathematics, 3, A. K. Peters, Wellesley, MA, 1993.Google Scholar
[AG] Anick, D. and Gray, B., Small H-spaces related to Moore spaces. Topology 34(1995), no. 4, 859–881. doi:10.1016/0040-9383(95)00001-1Google Scholar
[CMN1] Cohen, F. R., Moore, J. C., and Neisendorfer, J. A., Torsion in homotopy groups. Ann. of Math. 109(1979), no. 1, 121–168. doi:10.2307/1971269Google Scholar
[CMN2] Cohen, F. R., Moore, J. C., and Neisendorfer, J. A., The double suspension and exponents of the homotopy groups of spheres. Ann. of Math. 110(1979), no. 3, 549–565. doi:10.2307/1971238Google Scholar
[G] Gray, B., On the iterated suspension. Topology 27(1988), no. 3, 301–310. doi:10.1016/0040-9383(88)90011-0Google Scholar
[GT1] Gray, B. and Theriault, S., On the double suspension and the mod-p Moore space. In: An alpine anthology of homotopy theory, Contemp. Math., 399, American Mathematical Society, Providence, RI, 2006, pp. 101–121.Google Scholar
[GT2] Gray, B. and Theriault, S., An elementary construction of Anick's fibration. Geom. Topol. 14(2010), no. 1, 243–275. doi:10.2140/gt.2010.14.243Google Scholar
[N] Neisendorfer, J. A., Properties of certain H-spaces. Quart. J. Math. Oxford 34(1983), no. 134, 201–209. doi:10.1093/qmath/34.2.201Google Scholar
[S1] Selick, P., A decomposition of π* (S 2p +1 ; ℤ/pℤ). Topology 20(1981), no. 2, 175–177. doi:10.1016/0040-9383(81)90036-7Google Scholar
[S2] Selick, P., A reformulation of the Arf invariant one mod-p problem and applications to atomic spaces. Pacific J. Math. 108(1983), no. 2, 431–450.Google Scholar
[S3] Selick, P., Space exponents for loop spaces of spheres. In: Stable and unstable homotopy, Fields Inst. Commun., 19, American Mathematical Society, Providence, RI, 1998, 279–283.Google Scholar
[T] Theriault, S. D., The 3-primary classifying space of the fiber of the double suspension. Proc. Amer. Math. Soc. 136(2008), no. 4, 1489–1499. doi:10.1090/S0002-9939-07-09249-0Google Scholar