Canonical Vector Heights on Algebraic 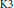$\text{K}3$ Surfaces with Picard Number Two

Abstract

Let 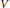$V$ be an algebraic 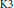$\text{K}3$ surface defined over a number field 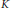$K$. Suppose 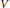$V$ has Picard number two and an infinite group of automorphisms 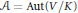$\mathcal{A}\,=\,\text{Aut(}V/K\text{)}$. In this paper, we introduce the notion of a vector height 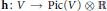$\mathbf{h}:\,V\,\to \,\text{Pic(}V\text{)}\,\otimes \,\mathbb{R}$ and show the existence of a canonical vector height 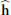$\mathbf{\hat{h}}$ with the following properties:

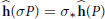$$\widehat{\mathbf{h}}\,\left( \sigma P \right)\,=\,{{\sigma }_{*}}\widehat{\mathbf{h}}\left( P \right)$$

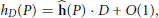$${{h}_{D}}(P)\,=\,\mathbf{\hat{h}}(P)\,\cdot \,D\,+\,O(1),$$

where 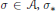$\sigma \,\in \,\mathcal{A},\,{{\sigma }_{*}}$ is the pushforward of 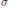$\sigma $ (the pullback of 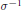${{\sigma }^{-1}}$), and 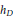${{h}_{D}}$ is a Weil height associated to the divisor 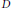$D$. The bounded function implied by the 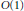$O(1)$ does not depend on $P$. This allows us to attack some arithmetic problems. For example, we show that the number of rational points with bounded logarithmic height in an 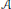$\mathcal{A}$-orbit satisfies

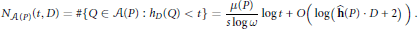$${{N}_{\mathcal{A}(P)}}(t,\,D)\,=\,\#\{Q\,\in \,\mathcal{A}(P)\,:\,{{h}_{D}}(Q)\,<\,t\}\,=\,\frac{\mu (P)}{s\,\log \,\omega }\,\log t\,+\,O\left( \log \left( \mathbf{\hat{h}}(P)\,\cdot \,D\,+\,2 \right) \right).$$

Here, 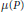$\mu (P)$ is a nonnegative integer, 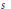$s$ is a positive integer, and $\omega $ is a real quadratic fundamental unit.