Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
LI, CAI HENG
and
WANG, LEI
2016.
RELATIVE ELEMENTARY ABELIAN GROUPS AND A CLASS OF EDGE-TRANSITIVE CAYLEY GRAPHS.
Journal of the Australian Mathematical Society,
Vol. 100,
Issue. 2,
p.
241.
Chen, Gang
and
Xu, Bangteng
2018.
Structures of commutative table algebras determined by their character tables and applications to finite groups.
Communications in Algebra,
Vol. 46,
Issue. 8,
p.
3510.
Lewis, Mark L.
2018.
Group Theory and Computation.
p.
141.
Chen, Gang
and
Xu, Bangteng
2019.
Generalized wreath products of table algebras determined by their character tables and applications to association schemes.
Discrete Mathematics,
Vol. 342,
Issue. 1,
p.
29.
Burkett, Shawn T.
and
Lewis, Mark L.
2020.
Groups where the centers of the irreducible characters form a chain II.
Monatshefte für Mathematik,
Vol. 192,
Issue. 4,
p.
783.
Burkett, Shawn T.
and
Lewis, Mark L.
2020.
Vanishing-off subgroups and supercharacter theory products.
International Journal of Algebra and Computation,
Vol. 30,
Issue. 05,
p.
1057.
Wang, Lei
and
Qiao, Shou Hong
2021.
Frobenius REA-groups and their Cayley graphs.
Journal of Algebra and Its Applications,
Vol. 20,
Issue. 02,
p.
2150007.
Burkett, Shawn T.
and
Lewis, Mark L.
2021.
A Frobenius group analog for Camina triples.
Journal of Algebra,
Vol. 568,
Issue. ,
p.
160.
Burkett, Shawn T.
and
Lewis, Mark L.
2024.
Corrigendum to “A Frobenius group analog for Camina triples” [J. Algebra 568 (2021) 160–180].
Journal of Algebra,
Vol. 649,
Issue. ,
p.
270.
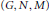 $(G,\,N,\,M)$ is a Camina triple, then either
$(G,\,N,\,M)$ is a Camina triple, then either 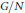 $G/N$ is a
$G/N$ is a 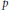 $p$-group, or
$p$-group, or 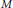 $M$ is abelian, or
$M$ is abelian, or 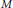 $M$ has a non-trivial nilpotent or Frobenius quotient.
$M$ has a non-trivial nilpotent or Frobenius quotient.