Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T12:05:20.098Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounds on Positive Integral Solutions of Linear Diophantine Equations II

Published online by Cambridge University Press:  20 November 2018

I. Borosh  and
L. B. Treybig
I. Borosh
Affiliation:
Department of Mathematics, Texas A & M University, College of Science, College Station, Texas 77840
L. B. Treybig
Affiliation:
Department of Mathematics, Texas A & M University, College of Science, College Station, Texas 77840
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let A be an m × n matrix of rank r and B an m × 1 matrix, both with integer entries. Let M2 be the maximum of the absolute values of the r × r minors of the augmented matrix (A | B). Suppose that the system A x = B has a non-trivial solution in non-negative integers. We prove (1) If r = n - 1 then the system A x = B has a non-negative non-trivial solution with entries bounded by M2. (2) If A has a r x n submatrix such that none of its r x r minors is 0 and x ≥ 0 is a solution of Ax=B in integers such that 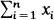is minimal, then .

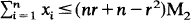Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 22 , Issue 3 , 01 September 1979 , pp. 357 - 361
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Borosh, I. and Treybig, L. B., Bounds on positive integral solutions of linear diophantine equations, Proceedings of the A.M.S. Vol. 55 Number 2 March 1976, 299-304.Google Scholar
2. Borosh, I., A sharp bound for positive solutions of homogeneous linear diophantine equations, Proceedings of the A.M.S. Vol. 60 October 1976, 19-21.Google Scholar
3. Haken, W., Théorie der Normal fiacken Acta. Math. 105 (1961), 245-375.Google Scholar
4. Schubert, H., Bestimmung der Primfaktorzerlegung von Verkettungen, Math. Zeit., 76 (1961), 116-148.Google Scholar
5. Treybig, L. B., Bounds in piecewise linear topology, Trans. Amer. Math. Soc, 201 (1975), 383-405.Google Scholar