Article contents
Boundedness in a Quasi-Uniform Space
Published online by Cambridge University Press: 20 November 2018
Extract
Although a nontopological concept, boundedness seems to be of considerable importance in a topological space. 'There are many topological problems in which it is essential to be able to make this distinction' (between bounded and unbounded sets) [1]. Boundedness and in particular boundedness-preserving' uniform spaces appear to have applications to topological dynamics [4].
In spite of this importance, there have been only isolated attempts at developing the concept. Alexander [1] and Hu [7] tried the axiomatic approach. Hu, for example, calls a nonempty family 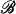 of sets a boundedness if
of sets a boundedness if  is hereditary and closed under finite union.
is hereditary and closed under finite union.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1970
References
- 5
- Cited by


