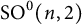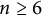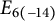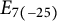1 Introduction
A group invariant is called profinite if it agrees for any two finitely generated residually finite groups
![]() $\Gamma , \Lambda $
with isomorphic profinite completions. A standard example is the abelianization
$\Gamma , \Lambda $
with isomorphic profinite completions. A standard example is the abelianization
![]() $H_1(\Gamma )$
; a more sophisticated example is largeness [Reference Lackenby20]. It seems, however, that more often than not, group invariants fail to be profinite. Kazhdan’s property
$H_1(\Gamma )$
; a more sophisticated example is largeness [Reference Lackenby20]. It seems, however, that more often than not, group invariants fail to be profinite. Kazhdan’s property
![]() $(T)$
[Reference Aka2], higher
$(T)$
[Reference Aka2], higher
![]() $\ell ^2$
-Betti numbers [Reference Kammeyer and Sauer15], Euler characteristic and
$\ell ^2$
-Betti numbers [Reference Kammeyer and Sauer15], Euler characteristic and
![]() $\ell ^2$
-torsion [Reference Kammeyer, Kionke, Raimbault and Sauer14], amenability [Reference Kionke and Schesler17], finiteness properties [Reference Lubotzky22], and most recently Serre’s Property FA [Reference Cheetham-West, Lubotzky, Reid and Spitler6] are all known not to be profinite. This list is by no means exhaustive and bounded cohomology is another item.
$\ell ^2$
-torsion [Reference Kammeyer, Kionke, Raimbault and Sauer14], amenability [Reference Kionke and Schesler17], finiteness properties [Reference Lubotzky22], and most recently Serre’s Property FA [Reference Cheetham-West, Lubotzky, Reid and Spitler6] are all known not to be profinite. This list is by no means exhaustive and bounded cohomology is another item.
Lemma 1 Let
![]() $\Gamma \kern1.2pt{=}\kern1.2pt \operatorname {Spin}(7,2)(\mathbb {Z})$
and
$\Gamma \kern1.2pt{=}\kern1.2pt \operatorname {Spin}(7,2)(\mathbb {Z})$
and
![]() $\Lambda \kern1.2pt{=}\kern1.2pt \operatorname {Spin}(3,6)(\mathbb {Z})$
. Then
$\Lambda \kern1.2pt{=}\kern1.2pt \operatorname {Spin}(3,6)(\mathbb {Z})$
. Then
![]() $\widehat {\Gamma } \kern1.2pt{\cong}\kern1.2pt \widehat {\Lambda }$
, but
$\widehat {\Gamma } \kern1.2pt{\cong}\kern1.2pt \widehat {\Lambda }$
, but
![]() $H^2_b(\Gamma; \mathbb {R}) \kern1.2pt{\cong} \mathbb {R}$
, while
$H^2_b(\Gamma; \mathbb {R}) \kern1.2pt{\cong} \mathbb {R}$
, while
![]() $H^2_b(\Lambda; \mathbb {R}) \cong 0$
.
$H^2_b(\Lambda; \mathbb {R}) \cong 0$
.
For an ad hoc definition of the spinor group
![]() $\operatorname {Spin}(q)(\mathcal {O})$
of a quadratic form q over an integral domain
$\operatorname {Spin}(q)(\mathcal {O})$
of a quadratic form q over an integral domain
![]() $\mathcal {O}$
, we refer to [Reference Kammeyer and Sauer15, Section 3]. The profinite completion
$\mathcal {O}$
, we refer to [Reference Kammeyer and Sauer15, Section 3]. The profinite completion
![]() $\widehat {\Gamma }$
of a group
$\widehat {\Gamma }$
of a group
![]() $\Gamma $
is the projective limit of the inverse system of finite quotient groups of
$\Gamma $
is the projective limit of the inverse system of finite quotient groups of
![]() $\Gamma $
. The bounded cohomology
$\Gamma $
. The bounded cohomology
![]() $H^*_b(\Gamma; \mathbb {R})$
with real coefficients of a discrete group
$H^*_b(\Gamma; \mathbb {R})$
with real coefficients of a discrete group
![]() $\Gamma $
is the cohomology of the cochain complex
$\Gamma $
is the cohomology of the cochain complex
![]() $\ell ^\infty (\Gamma ^{*+1}, \mathbb {R})^{\Gamma} $
, of bounded functions
$\ell ^\infty (\Gamma ^{*+1}, \mathbb {R})^{\Gamma} $
, of bounded functions
![]() $\Gamma ^{*+1} \rightarrow \mathbb {R}$
which are constant on the orbits of the diagonal
$\Gamma ^{*+1} \rightarrow \mathbb {R}$
which are constant on the orbits of the diagonal
![]() $\Gamma $
-action on
$\Gamma $
-action on
![]() $\Gamma ^{*+1}$
, with the usual differential. The reader may consult [Reference Frigerio7] for further details.
$\Gamma ^{*+1}$
, with the usual differential. The reader may consult [Reference Frigerio7] for further details.
Let us quickly prove the lemma. If the Witt index of an integral quadratic form q is at least 2, then
![]() $\operatorname {Spin}(q)(\mathbb {Z})$
has the congruence subgroup property (CSP). This implies that
$\operatorname {Spin}(q)(\mathbb {Z})$
has the congruence subgroup property (CSP). This implies that
The standard forms of signature
![]() $(7,2)$
and
$(7,2)$
and
![]() $(3,6)$
are isometric over
$(3,6)$
are isometric over
![]() $\mathbb {Z}_p$
for all (finite) primes p because standard quadratic form theory shows
$\mathbb {Z}_p$
for all (finite) primes p because standard quadratic form theory shows
Since
![]() $\operatorname {Spin}(q)(\mathcal {O})$
is functorial in isometries
$\operatorname {Spin}(q)(\mathcal {O})$
is functorial in isometries
![]() $q \cong _{\mathcal {O}} q'$
[Reference Kammeyer and Sauer15, Lemma 7], we conclude
$q \cong _{\mathcal {O}} q'$
[Reference Kammeyer and Sauer15, Lemma 7], we conclude
![]() $\widehat {\Gamma } \cong \widehat {\Lambda }$
. But the second bounded cohomology of higher-rank lattices was computed by Monod and Shalom [Reference Monod and Shalom24, Theorem 1.4], and it turns out that
$\widehat {\Gamma } \cong \widehat {\Lambda }$
. But the second bounded cohomology of higher-rank lattices was computed by Monod and Shalom [Reference Monod and Shalom24, Theorem 1.4], and it turns out that
![]() $H^2_b(\Gamma , \mathbb {R}) \cong \mathbb {R}$
, whereas
$H^2_b(\Gamma , \mathbb {R}) \cong \mathbb {R}$
, whereas
![]() $H^2_b(\Lambda , \mathbb {R}) \cong 0$
.
$H^2_b(\Lambda , \mathbb {R}) \cong 0$
.
This counterexample to the profiniteness of bounded cohomology is similar in spirit to Aka’s counterexamples to the profiniteness of Property (T) in [Reference Aka2]. Experts might have been aware of it, but we could not find a reference. In any case, it has prompted us to investigate thoroughly how often or rare such pairs of groups occur among higher-rank lattices. The purpose of this article is to give the complete picture.
To state the result, let us agree that by a higher-rank Lie group, we mean the group of real points
![]() $G = \mathbf {G}(\mathbb {R})$
of a connected almost
$G = \mathbf {G}(\mathbb {R})$
of a connected almost
![]() $\mathbb {R}$
-simple linear algebraic
$\mathbb {R}$
-simple linear algebraic
![]() $\mathbb {R}$
-group
$\mathbb {R}$
-group
![]() $\mathbf {G}$
with
$\mathbf {G}$
with
![]() $\operatorname {rank}_{\mathbb {R}} \mathbf {G} \ge 2$
. We say that G exhibits non-profinite second bounded cohomology if there exist a lattice
$\operatorname {rank}_{\mathbb {R}} \mathbf {G} \ge 2$
. We say that G exhibits non-profinite second bounded cohomology if there exist a lattice
![]() $\Gamma \le G$
and another lattice
$\Gamma \le G$
and another lattice
![]() $\Lambda \le H$
in some other higher-rank Lie group H such that
$\Lambda \le H$
in some other higher-rank Lie group H such that
![]() $\widehat {\Gamma } \cong \widehat {\Lambda }$
and such that
$\widehat {\Gamma } \cong \widehat {\Lambda }$
and such that
![]() $H^2_b(\Gamma; \mathbb {R}) \not \cong 0$
while
$H^2_b(\Gamma; \mathbb {R}) \not \cong 0$
while
![]() $H^2_b(\Lambda; \mathbb {R}) \cong 0$
.
$H^2_b(\Lambda; \mathbb {R}) \cong 0$
.
Theorem 2 Let G be a higher-rank Lie group. Then G exhibits non-profinite second bounded cohomology if and only if it is isogenous to
Here, we call two simple Lie groups isogenous if they have isomorphic Lie algebras. Note that a finite index subgroup of the group
![]() $\Gamma $
from Lemma 1 is a lattice in
$\Gamma $
from Lemma 1 is a lattice in
![]() $\operatorname {SO}^0(7,2)$
. The lemma actually provides the easiest possible example because the examples of lattices that we construct in
$\operatorname {SO}^0(7,2)$
. The lemma actually provides the easiest possible example because the examples of lattices that we construct in
![]() $\operatorname {SO}^0(6,2)$
come from triality forms of type
$\operatorname {SO}^0(6,2)$
come from triality forms of type
![]() $D_4$
, as we will see.
$D_4$
, as we will see.
Let us outline the proof of Theorem 2. The key result is the aforementioned theorem due to Monod and Shalom [Reference Monod and Shalom24, Theorem 1.4], which extends a previous result of Burger and Monod [Reference Burger and Monod4, Corollary 1.6]: for a lattice
![]() $\Gamma \le G$
in a higher-rank Lie group, we have
$\Gamma \le G$
in a higher-rank Lie group, we have
![]() $H^2_b(\Gamma; \mathbb {R}) \cong \mathbb {R}$
if
$H^2_b(\Gamma; \mathbb {R}) \cong \mathbb {R}$
if
![]() $\pi _1 G$
is infinite and
$\pi _1 G$
is infinite and
![]() $H^2_b(\Gamma; \mathbb {R}) \cong 0$
otherwise. It is well known that
$H^2_b(\Gamma; \mathbb {R}) \cong 0$
otherwise. It is well known that
![]() $\pi _1 G$
is infinite if and only if the symmetric space
$\pi _1 G$
is infinite if and only if the symmetric space
![]() $G/K$
associated with G is Hermitian [Reference Helgason11, Theorem VIII.6.1, p. 381]. The classification of Hermitian symmetric spaces is long-established [Reference Helgason11, Section X.6.3, p. 518]. The irreducible Hermitian symmetric spaces of higher rank are precisely the symmetric spaces of the simple Lie groups
$G/K$
associated with G is Hermitian [Reference Helgason11, Theorem VIII.6.1, p. 381]. The classification of Hermitian symmetric spaces is long-established [Reference Helgason11, Section X.6.3, p. 518]. The irreducible Hermitian symmetric spaces of higher rank are precisely the symmetric spaces of the simple Lie groups
 $$ \begin{gather*} \operatorname{SU}(n,m) \text{ for } n,m \ge 2, \ \operatorname{SO}^0(n,2) \text{ for } n \ge 3, \ \operatorname{SO}^*(2n) \text{ for } n \ge 4, \\ \operatorname{Sp}(n, \mathbb{R}) \text{ for } n \ge 2, \ E_{6(-14)}, \text{ and } \ E_{7(-25)}. \end{gather*} $$
$$ \begin{gather*} \operatorname{SU}(n,m) \text{ for } n,m \ge 2, \ \operatorname{SO}^0(n,2) \text{ for } n \ge 3, \ \operatorname{SO}^*(2n) \text{ for } n \ge 4, \\ \operatorname{Sp}(n, \mathbb{R}) \text{ for } n \ge 2, \ E_{6(-14)}, \text{ and } \ E_{7(-25)}. \end{gather*} $$
Here,
![]() $\operatorname {SO}^0(n,2)$
is the identity component of the determinant one matrices that preserve the standard quadratic form of signature
$\operatorname {SO}^0(n,2)$
is the identity component of the determinant one matrices that preserve the standard quadratic form of signature
![]() $(n,2)$
. The group
$(n,2)$
. The group
![]() $\operatorname {SO}^*(2n)$
is the quaternionic special orthogonal group as defined, for instance, in [Reference Morris25, Example A2.4.2, p. 430]. Using the symbol “
$\operatorname {SO}^*(2n)$
is the quaternionic special orthogonal group as defined, for instance, in [Reference Morris25, Example A2.4.2, p. 430]. Using the symbol “
![]() $\approx $
” for isogenous groups, we have the accidental isogenies
$\approx $
” for isogenous groups, we have the accidental isogenies
![]() $\operatorname {SO}^0(3,2) \approx \operatorname {Sp}(2;\mathbb {R})$
,
$\operatorname {SO}^0(3,2) \approx \operatorname {Sp}(2;\mathbb {R})$
,
![]() $\operatorname {SO}^0(4,2) \approx \operatorname {SU}(2,2)$
, and
$\operatorname {SO}^0(4,2) \approx \operatorname {SU}(2,2)$
, and
![]() $\operatorname {SO}^0(6,2) \approx \operatorname {SO}^*(8)$
. Let G be one of the groups in the list, and let
$\operatorname {SO}^0(6,2) \approx \operatorname {SO}^*(8)$
. Let G be one of the groups in the list, and let
![]() $\Gamma \le G$
be any lattice. By Margulis arithmeticity, we may assume
$\Gamma \le G$
be any lattice. By Margulis arithmeticity, we may assume
![]() $\Gamma $
is an arithmetic subgroup of a simply-connected simple algebraic group
$\Gamma $
is an arithmetic subgroup of a simply-connected simple algebraic group
![]() $\mathbf {G}$
over some totally real number field k such that
$\mathbf {G}$
over some totally real number field k such that
![]() $G \approx \mathbf {G}(k_v)$
for some real place v of k and such that
$G \approx \mathbf {G}(k_v)$
for some real place v of k and such that
![]() $\mathbf {G}$
is anisotropic at all other infinite places of k. The CSP translates the question whether there exists
$\mathbf {G}$
is anisotropic at all other infinite places of k. The CSP translates the question whether there exists
![]() $\Lambda \le H$
as in the theorem to whether there exists a simply-connected simple l-group
$\Lambda \le H$
as in the theorem to whether there exists a simply-connected simple l-group
![]() $\mathbf {H}$
, an isomorphism
$\mathbf {H}$
, an isomorphism
![]() $\mathbb {A}^f_k \cong \mathbb {A}^f_l$
of topological rings between the finite adele rings of k and l, and a corresponding isomorphism
$\mathbb {A}^f_k \cong \mathbb {A}^f_l$
of topological rings between the finite adele rings of k and l, and a corresponding isomorphism
![]() $\mathbf {G}(\mathbb {A}^f_k) \cong \mathbf {H}(\mathbb {A}^f_l)$
such that
$\mathbf {G}(\mathbb {A}^f_k) \cong \mathbf {H}(\mathbb {A}^f_l)$
such that
![]() $\mathbf {H}$
is anisotropic at all but one infinite place where it should be isogenous to a higher-rank Lie group outside the list. The technical achievement of this paper, beside filling in the details of the arguments thus far, is to solve this problem by Galois cohomological methods.
$\mathbf {H}$
is anisotropic at all but one infinite place where it should be isogenous to a higher-rank Lie group outside the list. The technical achievement of this paper, beside filling in the details of the arguments thus far, is to solve this problem by Galois cohomological methods.
We conclude the introduction with some comments on related work and open questions. By definition, bounded cohomology comes with a comparison map
![]() $H^*_b(\Gamma; \mathbb {R}) \longrightarrow H^*(\Gamma; \mathbb {R})$
. The kernel of this homomorphism is denoted by
$H^*_b(\Gamma; \mathbb {R}) \longrightarrow H^*(\Gamma; \mathbb {R})$
. The kernel of this homomorphism is denoted by
![]() $EH^*_b(\Gamma; \mathbb {R})$
and is called exact bounded cohomology. In degree two, we have the well-known interpretation that
$EH^*_b(\Gamma; \mathbb {R})$
and is called exact bounded cohomology. In degree two, we have the well-known interpretation that
![]() $EH^2_b(\Gamma; \mathbb {R})$
detects non-trivial quasimorphisms: maps
$EH^2_b(\Gamma; \mathbb {R})$
detects non-trivial quasimorphisms: maps
![]() $f \colon \Gamma \rightarrow \mathbb {R}$
for which there exists
$f \colon \Gamma \rightarrow \mathbb {R}$
for which there exists
![]() $D> 0$
with
$D> 0$
with
for all
![]() $g,h \in \Gamma $
such that f is not at bounded distance from an honest homomorphism [Reference Frigerio7, Section 2.3]. For lattices in higher-rank linear Lie groups, it was verified by Burger and Monod [Reference Burger and Monod5, Theorem 21] that the comparison map in degree 2 is injective. So the question whether the existence of non-trivial quasimorphisms is a profinite property remains open for now.
$g,h \in \Gamma $
such that f is not at bounded distance from an honest homomorphism [Reference Frigerio7, Section 2.3]. For lattices in higher-rank linear Lie groups, it was verified by Burger and Monod [Reference Burger and Monod5, Theorem 21] that the comparison map in degree 2 is injective. So the question whether the existence of non-trivial quasimorphisms is a profinite property remains open for now.
However, for lattices in rank one groups, the situation is different. On the one hand, a result of Fujiwara shows that such lattices admit many quasimorphisms [Reference Fujiwara8]. On the other hand, Serre conjectured that these lattices should not have the CSP, so an important ingredient to construct groups with isomorphic profinite completions would be missing. Yet lattices in the rank one groups
![]() $\operatorname {\mathrm {Sp}}(n, 1)$
and
$\operatorname {\mathrm {Sp}}(n, 1)$
and
![]() $F_{4(-20)}$
share many properties with higher-rank lattices which might suggest that they in fact do have CSP [Reference Lubotzky21, Section 4].
$F_{4(-20)}$
share many properties with higher-rank lattices which might suggest that they in fact do have CSP [Reference Lubotzky21, Section 4].
If
![]() $F_{4(-20)}$
has CSP, then having non-trivial exact second bounded cohomology, or equivalently having non-trivial quasimorphisms, is not a profinite property. Indeed, let
$F_{4(-20)}$
has CSP, then having non-trivial exact second bounded cohomology, or equivalently having non-trivial quasimorphisms, is not a profinite property. Indeed, let
![]() $\mathbf {F_4}$
be the unique simply-connected absolutely almost simple
$\mathbf {F_4}$
be the unique simply-connected absolutely almost simple
![]() $\mathbb {Q}$
-split linear algebraic
$\mathbb {Q}$
-split linear algebraic
![]() $\mathbb {Q}$
-group of type
$\mathbb {Q}$
-group of type
![]() $F_4$
. Since the Dynkin diagram of type
$F_4$
. Since the Dynkin diagram of type
![]() $F_4$
has no symmetries and the center of
$F_4$
has no symmetries and the center of
![]() $F_4$
is trivial, we have
$F_4$
is trivial, we have
![]() $\mathbf {F_4} \cong \operatorname {\mathrm {Ad}} \mathbf {F_4} \cong \operatorname {\mathrm {Aut}} \mathbf {F_4}$
. Therefore, the Hasse principle for simply-connected groups gives
$\mathbf {F_4} \cong \operatorname {\mathrm {Ad}} \mathbf {F_4} \cong \operatorname {\mathrm {Aut}} \mathbf {F_4}$
. Therefore, the Hasse principle for simply-connected groups gives
![]() $H^1(\mathbb {Q}, \operatorname {\mathrm {Aut}} \mathbf {F_4}) \cong H^1(\mathbb {R}, \operatorname {\mathrm {Aut}} \mathbf {F_4})$
, meaning that every real form of type
$H^1(\mathbb {Q}, \operatorname {\mathrm {Aut}} \mathbf {F_4}) \cong H^1(\mathbb {R}, \operatorname {\mathrm {Aut}} \mathbf {F_4})$
, meaning that every real form of type
![]() $F_4$
comes with a unique
$F_4$
comes with a unique
![]() $\mathbb {Q}$
-structure. Moreover, any two
$\mathbb {Q}$
-structure. Moreover, any two
![]() $\mathbb {Q}$
-groups of type
$\mathbb {Q}$
-groups of type
![]() $F_4$
are
$F_4$
are
![]() $\mathbb {Q}_p$
-split and hence
$\mathbb {Q}_p$
-split and hence
![]() $\mathbb {Q}_p$
-isomorphic for all finite primes p by Kneser’s theorem [Reference Kneser19]. Therefore, if
$\mathbb {Q}_p$
-isomorphic for all finite primes p by Kneser’s theorem [Reference Kneser19]. Therefore, if
![]() $F_{4(-20)}$
has CSP, we can find arithmetic lattices
$F_{4(-20)}$
has CSP, we can find arithmetic lattices
![]() $\Gamma \le F_{4(-20)}$
and
$\Gamma \le F_{4(-20)}$
and
![]() $\Lambda \le F_{4(4)}$
with
$\Lambda \le F_{4(4)}$
with
![]() $\widehat {\Gamma } \cong \widehat {\Lambda }$
, but
$\widehat {\Gamma } \cong \widehat {\Lambda }$
, but
![]() $EH_b^2(\Gamma; \mathbb {R}) \neq 0$
, while
$EH_b^2(\Gamma; \mathbb {R}) \neq 0$
, while
![]() $EH_b^2(\Lambda; \mathbb {R}) = 0$
.
$EH_b^2(\Lambda; \mathbb {R}) = 0$
.
Another notion from this circle of ideas is Ulam stability. Here, instead of
![]() $\mathbb {R}$
, we consider unitary groups
$\mathbb {R}$
, we consider unitary groups
![]() $U(n) = \{ A \in \operatorname {GL}_n(\mathbb {C}) \colon A^* = A^{-1} \}$
and define an
$U(n) = \{ A \in \operatorname {GL}_n(\mathbb {C}) \colon A^* = A^{-1} \}$
and define an
![]() $\varepsilon $
-homomorphism as a map
$\varepsilon $
-homomorphism as a map
![]() $f \colon \Gamma \rightarrow U(n)$
such that
$f \colon \Gamma \rightarrow U(n)$
such that
![]() $\|f(gh) - f(g)f(h)\| \le \varepsilon $
holds for all
$\|f(gh) - f(g)f(h)\| \le \varepsilon $
holds for all
![]() $g,h \in \Gamma $
where
$g,h \in \Gamma $
where
![]() $\|\cdot \|$
denotes the operator norm in
$\|\cdot \|$
denotes the operator norm in
![]() $M_n(\mathbb {C})$
. We say that
$M_n(\mathbb {C})$
. We say that
![]() $\Gamma $
is uniformly
$\Gamma $
is uniformly
![]() $U(n)$
-stable if there exists a function
$U(n)$
-stable if there exists a function
![]() $\delta = \delta (\varepsilon )$
with
$\delta = \delta (\varepsilon )$
with
![]() $\lim _{\varepsilon \rightarrow 0} \delta (\varepsilon ) = 0$
such that for all
$\lim _{\varepsilon \rightarrow 0} \delta (\varepsilon ) = 0$
such that for all
![]() $\varepsilon $
-homomorphisms
$\varepsilon $
-homomorphisms
![]() $f \colon \Gamma \rightarrow U(n)$
, there exists an honest homomorphism
$f \colon \Gamma \rightarrow U(n)$
, there exists an honest homomorphism
![]() $F \colon \Gamma \rightarrow U(n)$
such that for all
$F \colon \Gamma \rightarrow U(n)$
such that for all
![]() $g \in \Gamma $
, we have
$g \in \Gamma $
, we have
![]() $\|f(g)-F(g)\| \le \delta (\varepsilon )$
. We say that
$\|f(g)-F(g)\| \le \delta (\varepsilon )$
. We say that
![]() $\Gamma $
is Ulam stable if it is
$\Gamma $
is Ulam stable if it is
![]() $U(n)$
-stable for all
$U(n)$
-stable for all
![]() $n \ge 1$
.
$n \ge 1$
.
It is a straightforward consequence of the Burger–Monod theorem that lattices in higher-rank linear Lie groups are uniformly
![]() $U(1)$
-stable [Reference Glebsky, Lubotzky, Monod and Rangarajan10, Theorem 1.0.11]. Most recently, Glebsky, Lubotzky, Monod, and Rangarajan proved the far-reaching generalization that lattices in many higher-rank semisimple Lie groups G are Ulam stable [Reference Glebsky, Lubotzky, Monod and Rangarajan10, Theorem 0.0.5]. In fact, they are even uniformly stable with respect to more general metrics on
$U(1)$
-stable [Reference Glebsky, Lubotzky, Monod and Rangarajan10, Theorem 1.0.11]. Most recently, Glebsky, Lubotzky, Monod, and Rangarajan proved the far-reaching generalization that lattices in many higher-rank semisimple Lie groups G are Ulam stable [Reference Glebsky, Lubotzky, Monod and Rangarajan10, Theorem 0.0.5]. In fact, they are even uniformly stable with respect to more general metrics on
![]() $U(n)$
. Interestingly, the technical condition “property-
$U(n)$
. Interestingly, the technical condition “property-
![]() $G(\mathcal {Q}_1, \mathcal {Q}_2)$
” that G needs to satisfy to conclude this stability of lattices fails for
$G(\mathcal {Q}_1, \mathcal {Q}_2)$
” that G needs to satisfy to conclude this stability of lattices fails for
![]() $\operatorname {SO}^0(n,2)$
,
$\operatorname {SO}^0(n,2)$
,
![]() $E_{6(-14)}$
, and
$E_{6(-14)}$
, and
![]() $E_{7(-25)}$
by [Reference Glebsky, Lubotzky, Monod and Rangarajan10, Theorem 0.0.6], but it holds true for
$E_{7(-25)}$
by [Reference Glebsky, Lubotzky, Monod and Rangarajan10, Theorem 0.0.6], but it holds true for
![]() $E_{6(2)}$
and
$E_{6(2)}$
and
![]() $E_{7(7)}$
[Reference Glebsky, Lubotzky, Monod and Rangarajan10, Proof of Proposition 6.3.6]. (It seems to be open whether it holds for groups of type
$E_{7(7)}$
[Reference Glebsky, Lubotzky, Monod and Rangarajan10, Proof of Proposition 6.3.6]. (It seems to be open whether it holds for groups of type
![]() $\operatorname {SO}^0(p,q)$
with
$\operatorname {SO}^0(p,q)$
with
![]() $p,q \ge 3$
.) We will see below that
$p,q \ge 3$
.) We will see below that
![]() $E_{6(2)}$
and
$E_{6(2)}$
and
![]() $E_{7(7)}$
contain lattices which are profinitely isomorphic to lattices in
$E_{7(7)}$
contain lattices which are profinitely isomorphic to lattices in
![]() $E_{6(-14)}$
and
$E_{6(-14)}$
and
![]() $E_{7(-25)}$
, respectively. The authors actually entertain the idea that property-
$E_{7(-25)}$
, respectively. The authors actually entertain the idea that property-
![]() $G(\mathcal {Q}_1, \mathcal {Q}_2)$
might be necessary for Ulam stability [Reference Glebsky, Lubotzky, Monod and Rangarajan10, Section 7]. If that was true, our theorem would thus have the corollary that Ulam stability is not a profinite property.
$G(\mathcal {Q}_1, \mathcal {Q}_2)$
might be necessary for Ulam stability [Reference Glebsky, Lubotzky, Monod and Rangarajan10, Section 7]. If that was true, our theorem would thus have the corollary that Ulam stability is not a profinite property.
In Section 2, we prove the “if part” of Theorem 2, and in Section 3, we prove the “only if” part.
2 Proof of Theorem 2 – “if part”
In this section, we show that higher-rank Lie groups isogenous to
![]() $\operatorname {SO}^0(n,2)$
for
$\operatorname {SO}^0(n,2)$
for
![]() $n \ge 6$
,
$n \ge 6$
,
![]() $E_{6(-14)}$
, or
$E_{6(-14)}$
, or
![]() $E_{7(-25)}$
exhibit non-profinite second bounded cohomology. We start with the group
$E_{7(-25)}$
exhibit non-profinite second bounded cohomology. We start with the group
![]() $E_{7(-25)}$
.
$E_{7(-25)}$
.
Fix a prime number
![]() $p_0$
. Let
$p_0$
. Let
![]() $\mathbf {E_7}$
be the unique simply-connected absolutely almost simple
$\mathbf {E_7}$
be the unique simply-connected absolutely almost simple
![]() $\mathbb {Q}$
-split linear algebraic
$\mathbb {Q}$
-split linear algebraic
![]() $\mathbb {Q}$
-group of type
$\mathbb {Q}$
-group of type
![]() $E_7$
. The center
$E_7$
. The center
![]() $Z(\mathbf {E_7}) \cong \mu _2$
is isomorphic to the algebraic group of “second roots of unity” [Reference Platonov and Rapinchuk27, Table on p. 332], so that
$Z(\mathbf {E_7}) \cong \mu _2$
is isomorphic to the algebraic group of “second roots of unity” [Reference Platonov and Rapinchuk27, Table on p. 332], so that
![]() $\mu _2(K) = \{\pm 1\}$
for any field extension
$\mu _2(K) = \{\pm 1\}$
for any field extension
![]() $K/\mathbb {Q}$
. By [Reference Serre34, Section I.5.7], the corresponding equivariant short exact sequence of
$K/\mathbb {Q}$
. By [Reference Serre34, Section I.5.7], the corresponding equivariant short exact sequence of
![]() $\operatorname {Gal}(\mathbb {Q})$
-groups
$\operatorname {Gal}(\mathbb {Q})$
-groups
and functoriality yield a commuting diagram of Galois cohomology sets

which is exact at the middle term of each row. The direct sums in the upper row denote the subsets of the Cartesian products consisting of elements with all but finitely many coordinates equal to the unit class. We agree that the infinite prime
![]() $\infty $
with
$\infty $
with
![]() $\mathbb {Q}_\infty = \mathbb {R}$
is included. Let us collect some information on this diagram.
$\mathbb {Q}_\infty = \mathbb {R}$
is included. Let us collect some information on this diagram.
Proposition 3 The map f is surjective and
![]() $\Delta _{p_0}$
has trivial kernel.
$\Delta _{p_0}$
has trivial kernel.
Proof The surjectivity of f is implicit in the work of Borel and Harder [Reference Borel and Harder3] but can be cited explicitly from Prasad and Rapinchuk [Reference Prasad and Rapinchuk29, Proposition 1]. The map
![]() $\Delta _{p_0}$
has trivial kernel by exactness of the lower sequence and because
$\Delta _{p_0}$
has trivial kernel by exactness of the lower sequence and because
![]() $H^1(\mathbb {Q}_{p_0}, \mathbf {E_7}) = 0$
by a result of Kneser [Reference Kneser19].
$H^1(\mathbb {Q}_{p_0}, \mathbf {E_7}) = 0$
by a result of Kneser [Reference Kneser19].
Proposition 4 The image of
![]() $\pi _{\mathbb {R}} \colon H^1(\mathbb {R}, \mathbf {E_7}) \longrightarrow H^1(\mathbb {R}, \operatorname {Ad} \mathbf {E_7})$
consists of two elements, corresponding to the real forms
$\pi _{\mathbb {R}} \colon H^1(\mathbb {R}, \mathbf {E_7}) \longrightarrow H^1(\mathbb {R}, \operatorname {Ad} \mathbf {E_7})$
consists of two elements, corresponding to the real forms
![]() $E_{7(7)}$
and
$E_{7(7)}$
and
![]() $E_{7(-25)}$
.
$E_{7(-25)}$
.
Proof This was already observed as part of the investigation in [Reference Kammeyer and Spitler16], but let us give a direct argument for the convenience of the reader. By [Reference Serre34, Section I.5.7], the map
![]() $\pi _{\mathbb {R}}$
sits in the exact sequence
$\pi _{\mathbb {R}}$
sits in the exact sequence
By [Reference Serre34, Corollary 2, Section I.5.6], the map
![]() $\delta $
is a group homomorphism, hence
$\delta $
is a group homomorphism, hence
![]() $\operatorname {im} \delta \cong \operatorname {Ad} \mathbf {E_7}(\mathbb {R}) / p(\mathbf {E_7}(\mathbb {R}))$
by exactness. But the
$\operatorname {im} \delta \cong \operatorname {Ad} \mathbf {E_7}(\mathbb {R}) / p(\mathbf {E_7}(\mathbb {R}))$
by exactness. But the
![]() $\mathbb {R}$
-points of a simply-connected semisimple
$\mathbb {R}$
-points of a simply-connected semisimple
![]() $\mathbb {R}$
-group form a connected Lie group [Reference Margulis23, Remark (2), p. 52], whereas
$\mathbb {R}$
-group form a connected Lie group [Reference Margulis23, Remark (2), p. 52], whereas
![]() $\operatorname {Ad} \mathbf {E_7}(\mathbb {R})$
has two connected components according to [Reference Adams and Taïbi1, Table 5, p. 1095]. Since
$\operatorname {Ad} \mathbf {E_7}(\mathbb {R})$
has two connected components according to [Reference Adams and Taïbi1, Table 5, p. 1095]. Since
![]() $H^1(\mathbb {R}, \mu _2) \cong \mathbb {Z} / 2$
, it follows that
$H^1(\mathbb {R}, \mu _2) \cong \mathbb {Z} / 2$
, it follows that
![]() $\delta $
is surjective, so
$\delta $
is surjective, so
![]() $\operatorname {ker} \pi _{\mathbb {R}} = 1$
by exactness. By [Reference Adams and Taïbi1, Table 3, p. 1094], the set
$\operatorname {ker} \pi _{\mathbb {R}} = 1$
by exactness. By [Reference Adams and Taïbi1, Table 3, p. 1094], the set
![]() $H^1(\mathbb {R}, \mathbf {E_7})$
has two elements, so
$H^1(\mathbb {R}, \mathbf {E_7})$
has two elements, so
![]() $\pi _{\mathbb {R}}$
is injective. If
$\pi _{\mathbb {R}}$
is injective. If
![]() $[a] \in H^1(\mathbb {R}, \mathbf {E_7})$
denotes the nontrivial class, we conclude from [Reference Serre34, Corollary 2, Section I.5.5] that the
$[a] \in H^1(\mathbb {R}, \mathbf {E_7})$
denotes the nontrivial class, we conclude from [Reference Serre34, Corollary 2, Section I.5.5] that the
![]() ${}_a \operatorname {Ad} \mathbf {E_7}(\mathbb {R})$
-action on
${}_a \operatorname {Ad} \mathbf {E_7}(\mathbb {R})$
-action on
![]() $H^1(\mathbb {R}, \mu _2) \cong \mathbb {Z}/2$
is transitive; hence,
$H^1(\mathbb {R}, \mu _2) \cong \mathbb {Z}/2$
is transitive; hence,
![]() ${}_a \operatorname {Ad} \mathbf {E_7}(\mathbb {R})$
must be disconnected. By [Reference Adams and Taïbi1, Table 5, p. 1095], the Hermitian form
${}_a \operatorname {Ad} \mathbf {E_7}(\mathbb {R})$
must be disconnected. By [Reference Adams and Taïbi1, Table 5, p. 1095], the Hermitian form
![]() $E_{7(-25)}$
is the only non-split disconnected form, so
$E_{7(-25)}$
is the only non-split disconnected form, so
![]() ${}_a \operatorname {Ad} \mathbf {E_7}(\mathbb {R})$
is of type
${}_a \operatorname {Ad} \mathbf {E_7}(\mathbb {R})$
is of type
![]() $E_{7(-25)}$
. This shows that
$E_{7(-25)}$
. This shows that
![]() $\pi _{\mathbb {R}}([a]) \in H^1(\mathbb {R}, \operatorname {Ad} \mathbf {E_7})$
corresponds to the real form
$\pi _{\mathbb {R}}([a]) \in H^1(\mathbb {R}, \operatorname {Ad} \mathbf {E_7})$
corresponds to the real form
![]() $E_{7(-25)}$
. Of course, the unit class
$E_{7(-25)}$
. Of course, the unit class
![]() $1 \in H^1(\mathbb {R}, \operatorname {Ad} \mathbf {E_7})$
corresponds to the split form
$1 \in H^1(\mathbb {R}, \operatorname {Ad} \mathbf {E_7})$
corresponds to the split form
![]() $E_{7(7)}$
.
$E_{7(7)}$
.
The surjectivity of f according to Proposition 3 lets us find classes
![]() $\alpha , \beta \in H^1(\mathbb {Q}, \operatorname {Ad} \mathbf {E_7})$
such that both
$\alpha , \beta \in H^1(\mathbb {Q}, \operatorname {Ad} \mathbf {E_7})$
such that both
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
split at all finite primes p except possibly at
$\beta $
split at all finite primes p except possibly at
![]() $p_0$
and such that
$p_0$
and such that
![]() $\alpha $
corresponds to the real form
$\alpha $
corresponds to the real form
![]() $E_{7(-25)}$
at
$E_{7(-25)}$
at
![]() $\infty $
, whereas
$\infty $
, whereas
![]() $\beta $
corresponds to the real form
$\beta $
corresponds to the real form
![]() $E_{7(7)}$
at
$E_{7(7)}$
at
![]() $\infty $
.
$\infty $
.
Proposition 5 Both
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
also split at
$\beta $
also split at
![]() $p_0$
.
$p_0$
.
Proof Proposition 4 and exactness of the upper sequence in the above diagram show that
![]() $\bigoplus \Delta _p(f(\alpha )) = \bigoplus \Delta _p(f(\beta )) = 1$
. By commutativity, we have
$\bigoplus \Delta _p(f(\alpha )) = \bigoplus \Delta _p(f(\beta )) = 1$
. By commutativity, we have
![]() $b(\Delta (\alpha )) = b(\Delta (\beta )) = 1$
. The map b is injective as a special case of [Reference Prasad and Rapinchuk29, Theorem 3.(2)]. In fact, the injectivity is an immediate consequence of the extended Albert–Brauer–Hasse–Noether theorem from global class field theory, stating that we have a short exact sequence
$b(\Delta (\alpha )) = b(\Delta (\beta )) = 1$
. The map b is injective as a special case of [Reference Prasad and Rapinchuk29, Theorem 3.(2)]. In fact, the injectivity is an immediate consequence of the extended Albert–Brauer–Hasse–Noether theorem from global class field theory, stating that we have a short exact sequence
where s sums up local invariants. Indeed,
![]() $H^2(\mathbb {Q}, \mu _2)$
is the subgroup
$H^2(\mathbb {Q}, \mu _2)$
is the subgroup
![]() $\operatorname {Br}_2(\mathbb {Q})$
of the Brauer group
$\operatorname {Br}_2(\mathbb {Q})$
of the Brauer group
![]() $\operatorname {Br}(\mathbb {Q}) = H^2(\mathbb {Q}, \mathbf {GL_1})$
consisting of order two elements. It follows that
$\operatorname {Br}(\mathbb {Q}) = H^2(\mathbb {Q}, \mathbf {GL_1})$
consisting of order two elements. It follows that
![]() $\Delta (\alpha ) = \Delta (\beta ) = 1$
, so
$\Delta (\alpha ) = \Delta (\beta ) = 1$
, so
![]() $b_{p_0}(\Delta (\alpha )) = b_{p_0}(\Delta (\beta )) = 1$
. Since
$b_{p_0}(\Delta (\alpha )) = b_{p_0}(\Delta (\beta )) = 1$
. Since
![]() $\Delta _{p_0}$
has trivial kernel by Proposition 3, commutativity of the right lower square gives
$\Delta _{p_0}$
has trivial kernel by Proposition 3, commutativity of the right lower square gives
![]() $f_{p_0}(\alpha ) = f_{p_0}(\beta ) = 1$
.
$f_{p_0}(\alpha ) = f_{p_0}(\beta ) = 1$
.
As the Dynkin diagram of type
![]() $E_7$
comes with no symmetries, the set
$E_7$
comes with no symmetries, the set
![]() $H^1(\mathbb {Q}, \operatorname {Ad} \mathbf {E_7})$
classifies all
$H^1(\mathbb {Q}, \operatorname {Ad} \mathbf {E_7})$
classifies all
![]() $\mathbb {Q}$
-forms of type
$\mathbb {Q}$
-forms of type
![]() $E_7$
. The upshot of Proposition 5 is that the simply-connected
$E_7$
. The upshot of Proposition 5 is that the simply-connected
![]() $\mathbb {Q}$
-forms
$\mathbb {Q}$
-forms
![]() $\mathbf {G_1}$
and
$\mathbf {G_1}$
and
![]() $\mathbf {G_2}$
defined by
$\mathbf {G_2}$
defined by
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
, respectively, are split and thus isomorphic over
$\beta $
, respectively, are split and thus isomorphic over
![]() $\mathbb {Q}_p$
for all finite primes p. It then follows from [Reference Kammeyer and Kionke13, Lemmas 2.5 and 2.6] that we also have an isomorphism
$\mathbb {Q}_p$
for all finite primes p. It then follows from [Reference Kammeyer and Kionke13, Lemmas 2.5 and 2.6] that we also have an isomorphism
![]() $\mathbf {G_1} \cong \mathbf {G_2}$
of group schemes over the finite adele ring
$\mathbf {G_1} \cong \mathbf {G_2}$
of group schemes over the finite adele ring
![]() $\mathbb {A}^f_{\mathbb {Q}}$
. Moreover, neither
$\mathbb {A}^f_{\mathbb {Q}}$
. Moreover, neither
![]() $\mathbf {G_1}$
nor
$\mathbf {G_1}$
nor
![]() $\mathbf {G_2}$
is topologically simply-connected at the infinite place. Indeed, we have
$\mathbf {G_2}$
is topologically simply-connected at the infinite place. Indeed, we have
![]() $Z(\mathbf {G_1}(\mathbb {R})) \cong Z(\mathbf {G_2}(\mathbb {R})) \cong \{ \pm 1 \}$
. But according to [Reference Onishchik and Vinberg26, Table 10, p. 321], the simply-connected real Lie group of type
$Z(\mathbf {G_1}(\mathbb {R})) \cong Z(\mathbf {G_2}(\mathbb {R})) \cong \{ \pm 1 \}$
. But according to [Reference Onishchik and Vinberg26, Table 10, p. 321], the simply-connected real Lie group of type
![]() $E_{7(7)}$
has cyclic center of order four, while the simply-connected real Lie group of type
$E_{7(7)}$
has cyclic center of order four, while the simply-connected real Lie group of type
![]() $E_{7(-25)}$
has infinite cyclic center. (The latter is actually a consequence of
$E_{7(-25)}$
has infinite cyclic center. (The latter is actually a consequence of
![]() $E_{7(-25)}$
giving rise to a Hermitian symmetric space.) By [Reference Prasad and Rapinchuk28, Main Theorem], this implies that the metaplectic kernels of
$E_{7(-25)}$
giving rise to a Hermitian symmetric space.) By [Reference Prasad and Rapinchuk28, Main Theorem], this implies that the metaplectic kernels of
![]() $\mathbf {G_1}$
and
$\mathbf {G_1}$
and
![]() $\mathbf {G_2}$
are trivial. The surjectivity result for the map f comes with an additional statement on the existence of isotropic preimages [Reference Prasad and Rapinchuk29, Theorem 1 (iii)] which allows us to assume that
$\mathbf {G_2}$
are trivial. The surjectivity result for the map f comes with an additional statement on the existence of isotropic preimages [Reference Prasad and Rapinchuk29, Theorem 1 (iii)] which allows us to assume that
![]() $\operatorname {rank}_{\mathbb {Q}} \mathbf {G_1} = 3$
and
$\operatorname {rank}_{\mathbb {Q}} \mathbf {G_1} = 3$
and
![]() $\operatorname {rank}_{\mathbb {Q}} \mathbf {G_2} = 7$
. Therefore, the centrality of the congruence kernels of
$\operatorname {rank}_{\mathbb {Q}} \mathbf {G_2} = 7$
. Therefore, the centrality of the congruence kernels of
![]() $\mathbf {G}_1$
and
$\mathbf {G}_1$
and
![]() $\mathbf {G_2}$
follows from [Reference Raghunathan30]. Together with [Reference Platonov and Rapinchuk27, Theorems 9.1 and 9.15], we conclude that the congruence kernels of
$\mathbf {G_2}$
follows from [Reference Raghunathan30]. Together with [Reference Platonov and Rapinchuk27, Theorems 9.1 and 9.15], we conclude that the congruence kernels of
![]() $\mathbf {G_1}$
and
$\mathbf {G_1}$
and
![]() $\mathbf {G_2}$
are in fact trivial.
$\mathbf {G_2}$
are in fact trivial.
Let
![]() $\Gamma _0$
and
$\Gamma _0$
and
![]() $\Lambda _0$
be arithmetic subgroups of
$\Lambda _0$
be arithmetic subgroups of
![]() $\mathbf {G_1}$
and
$\mathbf {G_1}$
and
![]() $\mathbf {G_2}$
, respectively, which we may assume intersect the center trivially. Since the congruence kernel of
$\mathbf {G_2}$
, respectively, which we may assume intersect the center trivially. Since the congruence kernel of
![]() $\mathbf {G_1}$
is trivial, the profinite completion
$\mathbf {G_1}$
is trivial, the profinite completion
![]() $\widehat {\Gamma _0}$
agrees with the congruence completion
$\widehat {\Gamma _0}$
agrees with the congruence completion
![]() $\overline {\Gamma _0}$
. The latter is an open subgroup of
$\overline {\Gamma _0}$
. The latter is an open subgroup of
![]() $\mathbf {G_1}(\mathbb {A}^f_{\mathbb {Q}})$
by strong approximation. Similarly, under the isomorphism
$\mathbf {G_1}(\mathbb {A}^f_{\mathbb {Q}})$
by strong approximation. Similarly, under the isomorphism
![]() $\mathbf {G_1}(\mathbb {A}^f_{\mathbb {Q}}) \cong \mathbf {G_2}(\mathbb {A}^f_{\mathbb {Q}})$
, the group
$\mathbf {G_1}(\mathbb {A}^f_{\mathbb {Q}}) \cong \mathbf {G_2}(\mathbb {A}^f_{\mathbb {Q}})$
, the group
![]() $\widehat {\Lambda _0} = \overline {\Lambda _0}$
is embedded as another open subgroup in
$\widehat {\Lambda _0} = \overline {\Lambda _0}$
is embedded as another open subgroup in
![]() $\mathbf {G_1}(\mathbb {A}^f_{\mathbb {Q}})$
. We denote the open intersection of these two open subgroups by
$\mathbf {G_1}(\mathbb {A}^f_{\mathbb {Q}})$
. We denote the open intersection of these two open subgroups by
![]() $U \le \mathbf {G_1}(\mathbb {A}^f_{\mathbb {Q}})$
. Then, by [Reference Ribes and Zalesskii32, Proposition 3.2.2, p. 80, and Lemma 3.1.4, p. 77], the groups
$U \le \mathbf {G_1}(\mathbb {A}^f_{\mathbb {Q}})$
. Then, by [Reference Ribes and Zalesskii32, Proposition 3.2.2, p. 80, and Lemma 3.1.4, p. 77], the groups
![]() $\Gamma = \Gamma _0 \cap U$
and
$\Gamma = \Gamma _0 \cap U$
and
![]() $\Lambda = \Lambda _0 \cap U$
have finite index in
$\Lambda = \Lambda _0 \cap U$
have finite index in
![]() $\Gamma _0$
and
$\Gamma _0$
and
![]() $\Lambda _0$
, respectively, and
$\Lambda _0$
, respectively, and
![]() $\widehat {\Gamma } \cong U \cong \widehat {\Lambda }$
.
$\widehat {\Gamma } \cong U \cong \widehat {\Lambda }$
.
By the Borel–Harish-Chandra theorem [Reference Margulis23, Theorem I.3.2.7, p. 63],
![]() $\Gamma $
is a lattice in the Lie group
$\Gamma $
is a lattice in the Lie group
![]() $\mathbf {G_1}(\mathbb {R})$
, while
$\mathbf {G_1}(\mathbb {R})$
, while
![]() $\Lambda $
is a lattice in
$\Lambda $
is a lattice in
![]() $\mathbf {G_2}(\mathbb {R})$
. Since
$\mathbf {G_2}(\mathbb {R})$
. Since
![]() $\Gamma $
does not meet the center of
$\Gamma $
does not meet the center of
![]() $\mathbf {G_1}$
,
$\mathbf {G_1}$
,
![]() $\Gamma $
is also a lattice in any central quotient of
$\Gamma $
is also a lattice in any central quotient of
![]() $\mathbf {G_1}(\mathbb {R})$
. As we explained in the introduction, the Burger–Monod–Shalom theorem gives
$\mathbf {G_1}(\mathbb {R})$
. As we explained in the introduction, the Burger–Monod–Shalom theorem gives
![]() $H^2_b(\Gamma; \mathbb {R}) \cong \mathbb {R}$
and
$H^2_b(\Gamma; \mathbb {R}) \cong \mathbb {R}$
and
![]() $H^2_b(\Lambda; \mathbb {R}) \cong 0$
because
$H^2_b(\Lambda; \mathbb {R}) \cong 0$
because
![]() $\mathbf {G_1}(\mathbb {R})$
has type
$\mathbf {G_1}(\mathbb {R})$
has type
![]() $E_{7(-25)}$
, whereas
$E_{7(-25)}$
, whereas
![]() $\mathbf {G_2}(\mathbb {R})$
has type
$\mathbf {G_2}(\mathbb {R})$
has type
![]() $E_{7(7)}$
. This completes the proof that Lie groups of type
$E_{7(7)}$
. This completes the proof that Lie groups of type
![]() $E_{7(-25)}$
exhibit non-profinite second bounded cohomology.
$E_{7(-25)}$
exhibit non-profinite second bounded cohomology.
Remark 7 We are grateful to the anonymous referee who suggested to us the following alternative way to construct a
![]() $\mathbb {Q}$
-form
$\mathbb {Q}$
-form
![]() $\mathbf {G_1}$
of type
$\mathbf {G_1}$
of type
![]() $E_7$
which has type
$E_7$
which has type
![]() $E_{7(-25)}$
at the real place and splits at all finite places. Consider the standard quadratic form
$E_{7(-25)}$
at the real place and splits at all finite places. Consider the standard quadratic form
![]() $q = x_1 ^2 + \cdots + x_8^2$
of rank eight. It corresponds to an element
$q = x_1 ^2 + \cdots + x_8^2$
of rank eight. It corresponds to an element
![]() $\alpha _q \in H^1(\mathbb {Q}, \mathbf {SO}(4,4))$
because the discriminant of q and the standard form of signature
$\alpha _q \in H^1(\mathbb {Q}, \mathbf {SO}(4,4))$
because the discriminant of q and the standard form of signature
![]() $(4,4)$
are both trivial. The boundary map
$(4,4)$
are both trivial. The boundary map
![]() $\delta ^2 \colon H^1(\mathbb {Q}, \mathbf {SO}(4,4)) \longrightarrow \operatorname {Br}_2(\mathbb {Q})$
associated with the short exact sequence
$\delta ^2 \colon H^1(\mathbb {Q}, \mathbf {SO}(4,4)) \longrightarrow \operatorname {Br}_2(\mathbb {Q})$
associated with the short exact sequence
is given by the Hasse–Witt invariant [Reference Serre34, III.3.2.b, p. 141] so that
![]() ${\delta ^2(\alpha _q) = w_2(q) = 1}$
. Thus,
${\delta ^2(\alpha _q) = w_2(q) = 1}$
. Thus,
![]() $\alpha _q$
has a preimage
$\alpha _q$
has a preimage
![]() $\beta _q \in H^1(\mathbb {Q}, \mathbf {Spin}(4,4))$
. Via the obvious Dynkin diagram inclusion
$\beta _q \in H^1(\mathbb {Q}, \mathbf {Spin}(4,4))$
. Via the obvious Dynkin diagram inclusion
![]() $D_4 \subset E_7$
, the class
$D_4 \subset E_7$
, the class
![]() $\beta _q$
maps to a class in
$\beta _q$
maps to a class in
![]() $H^1(\mathbb {Q}, \mathbf {E_7})$
. The image in
$H^1(\mathbb {Q}, \mathbf {E_7})$
. The image in
![]() $H^1(\mathbb {Q}, \operatorname {Ad} \mathbf {E_7})$
thus defines a
$H^1(\mathbb {Q}, \operatorname {Ad} \mathbf {E_7})$
thus defines a
![]() $\mathbb {Q}$
-form
$\mathbb {Q}$
-form
![]() $\mathbf {G_1}$
of type
$\mathbf {G_1}$
of type
![]() $E_7$
which splits at every finite place and has the Satake–Tits index
$E_7$
which splits at every finite place and has the Satake–Tits index

at the real place by construction. This shows that
![]() $\mathbf {G_1}(\mathbb {R})$
is the Lie group
$\mathbf {G_1}(\mathbb {R})$
is the Lie group
![]() $E_{7(-25)}$
.
$E_{7(-25)}$
.
We now turn our attention to the group
![]() $E_{6(-14)}$
. Again, we fix a rational prime
$E_{6(-14)}$
. Again, we fix a rational prime
![]() $p_0$
. Let
$p_0$
. Let
![]() $\mathbf {{}^2 E_6}$
be any simply-connected absolutely almost simple quasisplit
$\mathbf {{}^2 E_6}$
be any simply-connected absolutely almost simple quasisplit
![]() $\mathbb {Q}$
-group which splits neither at
$\mathbb {Q}$
-group which splits neither at
![]() $p_0$
nor at
$p_0$
nor at
![]() $\infty $
. Such a form exists according to [Reference Borel and Harder3, Proposition, p. 58]. The Hasse principle for adjoint groups [Reference Platonov and Rapinchuk27, Theorem 6.22, p. 336] shows that the diagonal map
$\infty $
. Such a form exists according to [Reference Borel and Harder3, Proposition, p. 58]. The Hasse principle for adjoint groups [Reference Platonov and Rapinchuk27, Theorem 6.22, p. 336] shows that the diagonal map
is injective. But f is also surjective by [Reference Prasad and Rapinchuk29, Proposition 1] because at
![]() $p_0$
, the group
$p_0$
, the group
![]() $\mathbf {{}^2 E_6}$
has no inner twist, meaning that the set
$\mathbf {{}^2 E_6}$
has no inner twist, meaning that the set
![]() $H^1(\mathbb {Q}_{p_0}, \operatorname {Ad} \mathbf {{}^2 E_6})$
is trivial [Reference Platonov and Rapinchuk27, Proposition 6.15(1), p. 334].
$H^1(\mathbb {Q}_{p_0}, \operatorname {Ad} \mathbf {{}^2 E_6})$
is trivial [Reference Platonov and Rapinchuk27, Proposition 6.15(1), p. 334].
The set
![]() $H^1(\mathbb {R}, \operatorname {Ad} \mathbf {{}^2 E_6})$
has three elements corresponding to the quasisplit form
$H^1(\mathbb {R}, \operatorname {Ad} \mathbf {{}^2 E_6})$
has three elements corresponding to the quasisplit form
![]() $E_{6(2)}$
, the Hermitian form
$E_{6(2)}$
, the Hermitian form
![]() $E_{6(-14)}$
, and the compact form
$E_{6(-14)}$
, and the compact form
![]() $E_{6(-78)}$
as we infer one more time from [Reference Adams and Taïbi1, Table 3, p. 1094 and Remark in 10.3]. Let
$E_{6(-78)}$
as we infer one more time from [Reference Adams and Taïbi1, Table 3, p. 1094 and Remark in 10.3]. Let
![]() $\alpha , \beta \in H^1(\mathbb {Q}, \operatorname {Ad} \mathbf {{}^2 E_6})$
be the unique classes corresponding to
$\alpha , \beta \in H^1(\mathbb {Q}, \operatorname {Ad} \mathbf {{}^2 E_6})$
be the unique classes corresponding to
![]() $E_{6(-14)}$
and
$E_{6(-14)}$
and
![]() $E_{6(2)}$
at the infinite place, respectively, and which are trivial at all finite places. We denote the simply-connected
$E_{6(2)}$
at the infinite place, respectively, and which are trivial at all finite places. We denote the simply-connected
![]() $\mathbb {Q}$
-forms of
$\mathbb {Q}$
-forms of
![]() $\mathbf {{}^2 E_6}$
corresponding to
$\mathbf {{}^2 E_6}$
corresponding to
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
by
$\beta $
by
![]() $\mathbf {G_1}$
and
$\mathbf {G_1}$
and
![]() $\mathbf {G_2}$
. By construction,
$\mathbf {G_2}$
. By construction,
![]() $\mathbf {G_1}$
and
$\mathbf {G_1}$
and
![]() $\mathbf {G_2}$
are isomorphic over
$\mathbf {G_2}$
are isomorphic over
![]() $\mathbb {Q}_p$
for all finite primes p. From the tables [Reference Platonov and Rapinchuk27, p. 332] and [Reference Onishchik and Vinberg26, Table 10, p. 321], we infer that the centers of
$\mathbb {Q}_p$
for all finite primes p. From the tables [Reference Platonov and Rapinchuk27, p. 332] and [Reference Onishchik and Vinberg26, Table 10, p. 321], we infer that the centers of
![]() $\mathbf {G_1}(\mathbb {R})$
and
$\mathbf {G_1}(\mathbb {R})$
and
![]() $\mathbf {G_2}(\mathbb {R})$
have order three, whereas the centers of the simply-connected real Lie groups of types
$\mathbf {G_2}(\mathbb {R})$
have order three, whereas the centers of the simply-connected real Lie groups of types
![]() $E_{6(-14)}$
and
$E_{6(-14)}$
and
![]() $E_{6(2)}$
are infinite cyclic and of order six, respectively. So again, the metaplectic kernels of
$E_{6(2)}$
are infinite cyclic and of order six, respectively. So again, the metaplectic kernels of
![]() $\mathbf {G_1}$
and
$\mathbf {G_1}$
and
![]() $\mathbf {G_2}$
are trivial. It follows anew from [Reference Prasad and Rapinchuk29, Theorem 1(iii)] that
$\mathbf {G_2}$
are trivial. It follows anew from [Reference Prasad and Rapinchuk29, Theorem 1(iii)] that
![]() $\operatorname {rank}_{\mathbb {Q}} \mathbf {G_1} = 2$
and
$\operatorname {rank}_{\mathbb {Q}} \mathbf {G_1} = 2$
and
![]() $\operatorname {rank}_{\mathbb {Q}} \mathbf {G_2} = 4$
so that both congruence kernels are central by [Reference Raghunathan30]. Finally, the case of type
$\operatorname {rank}_{\mathbb {Q}} \mathbf {G_2} = 4$
so that both congruence kernels are central by [Reference Raghunathan30]. Finally, the case of type
![]() ${}^2 E_6$
, which was still excluded in [Reference Platonov and Rapinchuk27, Theorem 9.1, p. 512], was meanwhile settled by Gille [Reference Gille9]. So [Reference Platonov and Rapinchuk27, Theorem 9.15] shows that both
${}^2 E_6$
, which was still excluded in [Reference Platonov and Rapinchuk27, Theorem 9.1, p. 512], was meanwhile settled by Gille [Reference Gille9]. So [Reference Platonov and Rapinchuk27, Theorem 9.15] shows that both
![]() $\mathbf {G}_1$
and
$\mathbf {G}_1$
and
![]() $\mathbf {G}_2$
have trivial congruence kernel. With these remarks, the rest of the argument goes through as before and we conclude that
$\mathbf {G}_2$
have trivial congruence kernel. With these remarks, the rest of the argument goes through as before and we conclude that
![]() $E_{6(-14)}$
exhibits non-profinite second bounded cohomology.
$E_{6(-14)}$
exhibits non-profinite second bounded cohomology.
For the group
![]() $\operatorname {SO}^0(6,2)$
, we can actually argue similarly. We let
$\operatorname {SO}^0(6,2)$
, we can actually argue similarly. We let
![]() $\mathbf {{}^3 D_4}$
be a simply-connected absolutely almost simple quasisplit
$\mathbf {{}^3 D_4}$
be a simply-connected absolutely almost simple quasisplit
![]() $\mathbb {Q}$
-group that localizes to the quasisplit triality form of type
$\mathbb {Q}$
-group that localizes to the quasisplit triality form of type
![]() ${}^3 D_4$
at a fixed prime
${}^3 D_4$
at a fixed prime
![]() $p_0$
and that splits at
$p_0$
and that splits at
![]() $\infty $
. Note that the
$\infty $
. Note that the
![]() $\mathbb {Q}$
-group
$\mathbb {Q}$
-group
![]() $\mathbf {{}^3 D_4}$
can either have outer type
$\mathbf {{}^3 D_4}$
can either have outer type
![]() ${}^3 D_4$
or
${}^3 D_4$
or
![]() ${}^6 D_4$
. Since again
${}^6 D_4$
. Since again
![]() $H^1(\mathbb {Q}_{p_0}, \operatorname {Ad} \mathbf {{}^3 D_4})$
is trivial according to [Reference Platonov and Rapinchuk27, Proposition 6.15(1), p. 334], we have a pointed bijection
$H^1(\mathbb {Q}_{p_0}, \operatorname {Ad} \mathbf {{}^3 D_4})$
is trivial according to [Reference Platonov and Rapinchuk27, Proposition 6.15(1), p. 334], we have a pointed bijection
Hence, there exist
![]() $\mathbb {Q}$
-forms
$\mathbb {Q}$
-forms
![]() $\mathbf {G_1}$
and
$\mathbf {G_1}$
and
![]() $\mathbf {G_2}$
of
$\mathbf {G_2}$
of
![]() $\mathbf {{}^3 D_4}$
that localize to the inner forms
$\mathbf {{}^3 D_4}$
that localize to the inner forms
![]() $\operatorname {SO}^0(6,2)$
and
$\operatorname {SO}^0(6,2)$
and
![]() $\operatorname {SO}^0(4,4)$
at the real place, respectively, and to the trivial inner twist of
$\operatorname {SO}^0(4,4)$
at the real place, respectively, and to the trivial inner twist of
![]() $\mathbf {{}^3 D_4}$
at all finite places so that they are isomorphic over
$\mathbf {{}^3 D_4}$
at all finite places so that they are isomorphic over
![]() $\mathbb {Q}_p$
for all p. We have
$\mathbb {Q}_p$
for all p. We have
![]() $\operatorname {rank}_{\mathbb {Q}} \mathbf {G_1} = 1$
and
$\operatorname {rank}_{\mathbb {Q}} \mathbf {G_1} = 1$
and
![]() $\operatorname {rank}_{\mathbb {Q}} \mathbf {G_2} = 2$
, so both groups have central congruence kernel, this time by [Reference Raghunathan31]. The tables [Reference Platonov and Rapinchuk27, p. 332] and [Reference Onishchik and Vinberg26, Table 10, p. 320] show that
$\operatorname {rank}_{\mathbb {Q}} \mathbf {G_2} = 2$
, so both groups have central congruence kernel, this time by [Reference Raghunathan31]. The tables [Reference Platonov and Rapinchuk27, p. 332] and [Reference Onishchik and Vinberg26, Table 10, p. 320] show that
![]() $\mathbf {G_1}(\mathbb {R})$
and
$\mathbf {G_1}(\mathbb {R})$
and
![]() $\mathbf {G_2}(\mathbb {R})$
have trivial center, whereas the corresponding topological universal coverings have center isomorphic to
$\mathbf {G_2}(\mathbb {R})$
have trivial center, whereas the corresponding topological universal coverings have center isomorphic to
![]() $\mathbb {Z} \oplus \mathbb {Z} / 2$
and
$\mathbb {Z} \oplus \mathbb {Z} / 2$
and
![]() $(\mathbb {Z}/2)^3$
, respectively. This implies that the metaplectic kernels of
$(\mathbb {Z}/2)^3$
, respectively. This implies that the metaplectic kernels of
![]() $\mathbf {G_1}$
and
$\mathbf {G_1}$
and
![]() $\mathbf {G_2}$
are trivial and so are the congruence kernels. Hence, we can once more construct profinitely isomorphic lattices in
$\mathbf {G_2}$
are trivial and so are the congruence kernels. Hence, we can once more construct profinitely isomorphic lattices in
![]() $\mathbf {G_1}(\mathbb {R})$
and
$\mathbf {G_1}(\mathbb {R})$
and
![]() $\mathbf {G_2}(\mathbb {R})$
as we did in type
$\mathbf {G_2}(\mathbb {R})$
as we did in type
![]() $E_7$
and we conclude that
$E_7$
and we conclude that
![]() $\operatorname {SO}^0(6,2) \approx \operatorname {SO}^*(8)$
exhibits non-profinite second bounded cohomology.
$\operatorname {SO}^0(6,2) \approx \operatorname {SO}^*(8)$
exhibits non-profinite second bounded cohomology.
Finally, we observe that Lemma 1 generalizes effortlessly to the groups
![]() ${\Gamma = \operatorname {Spin}(n,2)(\mathbb {Z})}$
and
${\Gamma = \operatorname {Spin}(n,2)(\mathbb {Z})}$
and
![]() $\Lambda = \operatorname {Spin}(n-4,6)(\mathbb {Z})$
for
$\Lambda = \operatorname {Spin}(n-4,6)(\mathbb {Z})$
for
![]() $n \ge 7$
. Let
$n \ge 7$
. Let
![]() $\Gamma _0 \le \Gamma $
be a finite index subgroup which intersects the center of
$\Gamma _0 \le \Gamma $
be a finite index subgroup which intersects the center of
![]() $\operatorname {Spin}(n,2)(\mathbb {R})$
trivially. Setting
$\operatorname {Spin}(n,2)(\mathbb {R})$
trivially. Setting
![]() $\Lambda _0 = \Lambda \cap \overline {\Gamma _0} \subset \widehat {\Gamma } \cong \widehat {\Lambda }$
, we have
$\Lambda _0 = \Lambda \cap \overline {\Gamma _0} \subset \widehat {\Gamma } \cong \widehat {\Lambda }$
, we have
![]() $\widehat {\Gamma _0} \cong \widehat {\Lambda _0}$
. The group
$\widehat {\Gamma _0} \cong \widehat {\Lambda _0}$
. The group
![]() $\Gamma _0$
is a lattice in every quotient group of
$\Gamma _0$
is a lattice in every quotient group of
![]() $\operatorname {Spin}(n,2)(\mathbb {R})$
by a central subgroup so that all Lie groups isogenous to
$\operatorname {Spin}(n,2)(\mathbb {R})$
by a central subgroup so that all Lie groups isogenous to
![]() $\operatorname {SO}^0(n,2)$
exhibit non-profinite second bounded cohomology for
$\operatorname {SO}^0(n,2)$
exhibit non-profinite second bounded cohomology for
![]() $n \ge 7$
.
$n \ge 7$
.
3 Proof of Theorem 2 – “only if part”
In this section, we show that the remaining higher-rank Lie groups defining Hermitian symmetric spaces
do not exhibit non-profinite second bounded cohomology. Recall that the group
![]() $\operatorname {SO}^0(3,2)$
is isogenous to
$\operatorname {SO}^0(3,2)$
is isogenous to
![]() $\operatorname {Sp}(2, \mathbb {R})$
and the group
$\operatorname {Sp}(2, \mathbb {R})$
and the group
![]() $\operatorname {SO}^0(4,2)$
is isogenous to
$\operatorname {SO}^0(4,2)$
is isogenous to
![]() $\operatorname {SU}(2,2)$
.
$\operatorname {SU}(2,2)$
.
As preparation, let k and l be totally real number fields and let
![]() $\mathbf {G}$
and
$\mathbf {G}$
and
![]() $\mathbf {H}$
be simply-connected absolutely almost simple groups defined over k and l, respectively. Assume that
$\mathbf {H}$
be simply-connected absolutely almost simple groups defined over k and l, respectively. Assume that
![]() $\mathbf {G}$
is anisotropic at all infinite places of k except one which we call v and that
$\mathbf {G}$
is anisotropic at all infinite places of k except one which we call v and that
![]() $\mathbf {H}$
is anisotropic at all infinite places of l except one which we call w. Suppose moreover that
$\mathbf {H}$
is anisotropic at all infinite places of l except one which we call w. Suppose moreover that
![]() $\operatorname {rank}_{k_v} \mathbf {G} \ge 2$
and
$\operatorname {rank}_{k_v} \mathbf {G} \ge 2$
and
![]() $\operatorname {rank}_{l_w} \mathbf {H} \ge 2$
and that there exist arithmetic subgroups
$\operatorname {rank}_{l_w} \mathbf {H} \ge 2$
and that there exist arithmetic subgroups
![]() $\Gamma \le \mathbf {G}(k)$
and
$\Gamma \le \mathbf {G}(k)$
and
![]() $\Lambda \le \mathbf {H}(l)$
such that
$\Lambda \le \mathbf {H}(l)$
such that
![]() $\widehat {\Gamma } \cong \widehat {\Lambda }$
. By adelic superrigidity [Reference Kammeyer and Kionke13, Theorem 3.4], we have an isomorphism
$\widehat {\Gamma } \cong \widehat {\Lambda }$
. By adelic superrigidity [Reference Kammeyer and Kionke13, Theorem 3.4], we have an isomorphism
![]() $j \colon \mathbb {A}^f_l \rightarrow \mathbb {A}^f_k$
of topological rings and a group scheme isomorphism
$j \colon \mathbb {A}^f_l \rightarrow \mathbb {A}^f_k$
of topological rings and a group scheme isomorphism
![]() $\eta \colon \mathbf {G} \times _k \mathbb {A}^f_k \longrightarrow \mathbf {H} \times _l \mathbb {A}^f_l$
over j. By the proof of [Reference Klingen18, Proposition 2.5(a), p. 238], the isomorphism j induces a bijection
$\eta \colon \mathbf {G} \times _k \mathbb {A}^f_k \longrightarrow \mathbf {H} \times _l \mathbb {A}^f_l$
over j. By the proof of [Reference Klingen18, Proposition 2.5(a), p. 238], the isomorphism j induces a bijection
![]() $u \mapsto u'$
of the finite places of k and l and isomorphisms
$u \mapsto u'$
of the finite places of k and l and isomorphisms
![]() $k_u \cong l_{u'}$
. Correspondingly, the isomorphism
$k_u \cong l_{u'}$
. Correspondingly, the isomorphism
![]() $\eta $
over j splits into a family of isomorphisms
$\eta $
over j splits into a family of isomorphisms
![]() $\mathbf {G}(k_u) \cong \mathbf {H}(l_{u'})$
. In particular,
$\mathbf {G}(k_u) \cong \mathbf {H}(l_{u'})$
. In particular,
![]() $\mathbf {G}$
and
$\mathbf {G}$
and
![]() $\mathbf {H}$
have the same Cartan Killing type.
$\mathbf {H}$
have the same Cartan Killing type.
Proposition 8 The
![]() $\mathbb {R}$
-groups
$\mathbb {R}$
-groups
![]() $\mathbf {G}_v$
and
$\mathbf {G}_v$
and
![]() $\mathbf {H}_w$
are inner twists of one another.
$\mathbf {H}_w$
are inner twists of one another.
Proof The case
![]() $k = l = \mathbb {Q}$
was handled in [Reference Kammeyer, Kionke, Raimbault and Sauer14, Proposition 2.7] (and it is apparent that the same arguments give the case of
$k = l = \mathbb {Q}$
was handled in [Reference Kammeyer, Kionke, Raimbault and Sauer14, Proposition 2.7] (and it is apparent that the same arguments give the case of
![]() $k=l$
if
$k=l$
if
![]() $v=w$
). For the general case, we argue as follows. Let
$v=w$
). For the general case, we argue as follows. Let
![]() $\mathbf {G_0}$
be the up to
$\mathbf {G_0}$
be the up to
![]() $\mathbb {Q}$
-isomorphism unique
$\mathbb {Q}$
-isomorphism unique
![]() $\mathbb {Q}$
-split simply-connected
$\mathbb {Q}$
-split simply-connected
![]() $\mathbb {Q}$
-group of the same Cartan Killing type as
$\mathbb {Q}$
-group of the same Cartan Killing type as
![]() $\mathbf {G}$
and
$\mathbf {G}$
and
![]() $\mathbf {H}$
. Let
$\mathbf {H}$
. Let
![]() $\mathbf {T} \subset \mathbf {G_0}$
be a maximal
$\mathbf {T} \subset \mathbf {G_0}$
be a maximal
![]() $\mathbb {Q}$
-split torus, pick a set
$\mathbb {Q}$
-split torus, pick a set
![]() $\Delta $
of simple roots of
$\Delta $
of simple roots of
![]() $\mathbf {G_0}$
with respect to
$\mathbf {G_0}$
with respect to
![]() $\mathbf {T}$
, and let
$\mathbf {T}$
, and let
![]() $\operatorname {Sym} \Delta $
be the subgroup of the permutation group of
$\operatorname {Sym} \Delta $
be the subgroup of the permutation group of
![]() $\Delta $
given by Dynkin diagram symmetries. Then we have a split short exact sequence
$\Delta $
given by Dynkin diagram symmetries. Then we have a split short exact sequence
of
![]() $\operatorname {Gal}(\mathbb {Q})$
-groups where
$\operatorname {Gal}(\mathbb {Q})$
-groups where
![]() $\operatorname {Gal}(\mathbb {Q})$
acts trivially on
$\operatorname {Gal}(\mathbb {Q})$
acts trivially on
![]() $\operatorname {Sym} \Delta $
. The group
$\operatorname {Sym} \Delta $
. The group
![]() $\mathbf {G}$
corresponds to a unique class
$\mathbf {G}$
corresponds to a unique class
![]() $\alpha \in H^1(k, \operatorname {Aut} \mathbf {G_0})$
and similarly
$\alpha \in H^1(k, \operatorname {Aut} \mathbf {G_0})$
and similarly
![]() $\mathbf {H}$
corresponds to a unique class
$\mathbf {H}$
corresponds to a unique class
![]() $\beta \in H^1(l, \operatorname {Aut} \mathbf {G_0})$
. Since we have isomorphisms
$\beta \in H^1(l, \operatorname {Aut} \mathbf {G_0})$
. Since we have isomorphisms
![]() $\mathbf {G}(k_u) \cong \mathbf {H}(l_{u'})$
, it follows by functoriality that
$\mathbf {G}(k_u) \cong \mathbf {H}(l_{u'})$
, it follows by functoriality that
![]() $\pi _* \alpha \in H^1(k, \operatorname {Sym} \Delta )$
and
$\pi _* \alpha \in H^1(k, \operatorname {Sym} \Delta )$
and
![]() $\pi _* \beta \in H^1(l, \operatorname {Sym} \Delta )$
map diagonally to corresponding elements under the induced isomorphism
$\pi _* \beta \in H^1(l, \operatorname {Sym} \Delta )$
map diagonally to corresponding elements under the induced isomorphism
Let us now first suppose that
![]() $\mathbf {G}$
and hence
$\mathbf {G}$
and hence
![]() $\mathbf {G_0}$
do not have type
$\mathbf {G_0}$
do not have type
![]() $D_4$
. We may then assume that
$D_4$
. We may then assume that
![]() $\operatorname {Sym} \Delta \cong \mathbb {Z} / 2\mathbb {Z}$
because the proposition is trivial if
$\operatorname {Sym} \Delta \cong \mathbb {Z} / 2\mathbb {Z}$
because the proposition is trivial if
![]() $\operatorname {Sym} \Delta $
is. Note that the first Galois cohomology with coefficients in
$\operatorname {Sym} \Delta $
is. Note that the first Galois cohomology with coefficients in
![]() $\mathbb {Z}/2\mathbb {Z}$
classifies quadratic field extensions. So we conclude that
$\mathbb {Z}/2\mathbb {Z}$
classifies quadratic field extensions. So we conclude that
![]() $\pi _* \alpha $
and
$\pi _* \alpha $
and
![]() $\pi _* \beta $
correspond to quadratic extensions
$\pi _* \beta $
correspond to quadratic extensions
![]() $K/k$
and
$K/k$
and
![]() $L/l$
, respectively, such that
$L/l$
, respectively, such that
![]() $\mathbb {A}^f_K \cong _{\mathbb {A}^f_{\mathbb {Q}}} \mathbb {A}^f_L$
(using [Reference Klingen18, Theorem 2.3, p. 237]). This shows in particular that K and L have the same number of real embeddings [Reference Klingen18, Theorem 1.4(h), p. 79]. It follows that the number of real places in k extending to complex places in K equals the number of real places in l extending to complex places in L. Translating back from field extensions to Galois cohomology classes, this shows that
$\mathbb {A}^f_K \cong _{\mathbb {A}^f_{\mathbb {Q}}} \mathbb {A}^f_L$
(using [Reference Klingen18, Theorem 2.3, p. 237]). This shows in particular that K and L have the same number of real embeddings [Reference Klingen18, Theorem 1.4(h), p. 79]. It follows that the number of real places in k extending to complex places in K equals the number of real places in l extending to complex places in L. Translating back from field extensions to Galois cohomology classes, this shows that
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
localize to outer forms at the same number of infinite places. Since
$\beta $
localize to outer forms at the same number of infinite places. Since
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
localize to the compact real form (which may be inner or outer depending on the Cartan Killing type) at all other infinite places,
$\beta $
localize to the compact real form (which may be inner or outer depending on the Cartan Killing type) at all other infinite places,
![]() $\alpha _v$
and
$\alpha _v$
and
![]() $\beta _w$
must be either both outer or both inner forms. In any case, they are inner twists of each other.
$\beta _w$
must be either both outer or both inner forms. In any case, they are inner twists of each other.
Now, if
![]() $\mathbf {G}$
and hence
$\mathbf {G}$
and hence
![]() $\mathbf {G_0}$
does have type
$\mathbf {G_0}$
does have type
![]() $D_4$
, then
$D_4$
, then
![]() $\operatorname {Sym} \Delta \cong S_3 \cong \mathbb {Z} / 3 \rtimes \mathbb {Z} / 2 $
. Note that subgroups of the same order are conjugate in this group. Therefore, the first Galois cohomology with coefficients in the trivial Galois module
$\operatorname {Sym} \Delta \cong S_3 \cong \mathbb {Z} / 3 \rtimes \mathbb {Z} / 2 $
. Note that subgroups of the same order are conjugate in this group. Therefore, the first Galois cohomology with coefficients in the trivial Galois module
![]() $S_3$
classifies Galois extensions with Galois groups either
$S_3$
classifies Galois extensions with Galois groups either
![]() $\mathbb {Z} / 2$
, or
$\mathbb {Z} / 2$
, or
![]() $\mathbb {Z} / 3$
, or
$\mathbb {Z} / 3$
, or
![]() $S_3$
(or trivial). So
$S_3$
(or trivial). So
![]() $\pi _* \alpha $
and
$\pi _* \alpha $
and
![]() $\pi _* \beta $
correspond to Galois extensions
$\pi _* \beta $
correspond to Galois extensions
![]() $K/k$
and
$K/k$
and
![]() $L/l$
of one and the same of these types, again such that
$L/l$
of one and the same of these types, again such that
![]() $\mathbb {A}^f_K \cong _{\mathbb {A}^f_{\mathbb {Q}}} \mathbb {A}^f_L$
. So once more, K and L have the same number of real embeddings. As K and L are Galois over k and l, respectively, real places extend either only to real places or only to complex places in these extensions. Correspondingly,
$\mathbb {A}^f_K \cong _{\mathbb {A}^f_{\mathbb {Q}}} \mathbb {A}^f_L$
. So once more, K and L have the same number of real embeddings. As K and L are Galois over k and l, respectively, real places extend either only to real places or only to complex places in these extensions. Correspondingly,
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
localize to outer forms again at the same number of infinite places of k and l. As all nontrivial homomorphisms
$\beta $
localize to outer forms again at the same number of infinite places of k and l. As all nontrivial homomorphisms
![]() $\operatorname {Gal} (\mathbb {R}) \rightarrow \operatorname {Sym} \Delta $
are conjugate, any two real outer forms are inner twists of each other even in type
$\operatorname {Gal} (\mathbb {R}) \rightarrow \operatorname {Sym} \Delta $
are conjugate, any two real outer forms are inner twists of each other even in type
![]() $D_4$
. It follows again that
$D_4$
. It follows again that
![]() $\alpha _v$
and
$\alpha _v$
and
![]() $\beta _w$
must be inner twists of one another.
$\beta _w$
must be inner twists of one another.
Now, let G be one of the groups listed at the beginning of this section and let
![]() $\Gamma \le G$
be a lattice. Let
$\Gamma \le G$
be a lattice. Let
![]() $\Lambda \le H$
be a lattice in another higher-rank Lie group and assume that
$\Lambda \le H$
be a lattice in another higher-rank Lie group and assume that
![]() $\widehat {\Gamma } \cong \widehat {\Lambda }$
. We have to show that H also defines a Hermitian symmetric space. By Margulis arithmeticity [Reference Margulis23, Chapter IX, Theorem 1.11, p. 298, (**), and Remark 1.6(i), pp. 293–294], there exist a k-group
$\widehat {\Gamma } \cong \widehat {\Lambda }$
. We have to show that H also defines a Hermitian symmetric space. By Margulis arithmeticity [Reference Margulis23, Chapter IX, Theorem 1.11, p. 298, (**), and Remark 1.6(i), pp. 293–294], there exist a k-group
![]() $\mathbf {G}$
and an l-group
$\mathbf {G}$
and an l-group
![]() $\mathbf {H}$
with k, l,
$\mathbf {H}$
with k, l,
![]() $\mathbf {G}$
, and
$\mathbf {G}$
, and
![]() $\mathbf {H}$
as above such that
$\mathbf {H}$
as above such that
![]() $\mathbf {G}_v$
is isogenous to G,
$\mathbf {G}_v$
is isogenous to G,
![]() $\mathbf {H}_w$
is isogenous to H, and
$\mathbf {H}_w$
is isogenous to H, and
![]() $\mathbf {G}(\mathcal {O}_k)$
is commensurable with
$\mathbf {G}(\mathcal {O}_k)$
is commensurable with
![]() $\Gamma $
while
$\Gamma $
while
![]() $\mathbf {H}(\mathcal {O}_l)$
is commensurable with
$\mathbf {H}(\mathcal {O}_l)$
is commensurable with
![]() $\Lambda $
. Since
$\Lambda $
. Since
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Lambda $
are profinitely isomorphic, so are suitable finite index subgroups of
$\Lambda $
are profinitely isomorphic, so are suitable finite index subgroups of
![]() $\mathbf {G}(\mathcal {O}_k)$
and
$\mathbf {G}(\mathcal {O}_k)$
and
![]() $\mathbf {H}(\mathcal {O}_l)$
. Therefore, we have the conclusion from above that there exist an isomorphism
$\mathbf {H}(\mathcal {O}_l)$
. Therefore, we have the conclusion from above that there exist an isomorphism
![]() $j \colon \mathbb {A}^f_l \rightarrow \mathbb {A}^f_k$
and an isomorphism
$j \colon \mathbb {A}^f_l \rightarrow \mathbb {A}^f_k$
and an isomorphism
![]() $\eta \colon \mathbf {G} \times _k \mathbb {A}^f_k \longrightarrow \mathbf {H} \times _l \mathbb {A}^f_l$
over j and Proposition 8 holds true for
$\eta \colon \mathbf {G} \times _k \mathbb {A}^f_k \longrightarrow \mathbf {H} \times _l \mathbb {A}^f_l$
over j and Proposition 8 holds true for
![]() $\mathbf {G}$
and
$\mathbf {G}$
and
![]() $\mathbf {H}$
.
$\mathbf {H}$
.
Proposition 10 The groups
![]() $G \approx \operatorname {SU}(n,m)$
with
$G \approx \operatorname {SU}(n,m)$
with
![]() $n, m \ge 2$
do not exhibit non-profinite second bounded cohomology.
$n, m \ge 2$
do not exhibit non-profinite second bounded cohomology.
Proof By Proposition 8, the group
![]() $\mathbf {H}_w$
is an inner twist of
$\mathbf {H}_w$
is an inner twist of
![]() $\mathbf {G}_v$
; hence, H is isogenous to
$\mathbf {G}_v$
; hence, H is isogenous to
![]() $\operatorname {SU}(n',m')$
for some
$\operatorname {SU}(n',m')$
for some
![]() $n',m' \ge 2$
because the generalized special unitary groups are the only outer real forms of type
$n',m' \ge 2$
because the generalized special unitary groups are the only outer real forms of type
![]() $A_n$
in the classification of real simple Lie groups. So H defines a Hermitian symmetric space, too.
$A_n$
in the classification of real simple Lie groups. So H defines a Hermitian symmetric space, too.
Proposition 11 The groups
![]() $G \approx \operatorname {Sp}(n, \mathbb {R})$
with
$G \approx \operatorname {Sp}(n, \mathbb {R})$
with
![]() $n \ge 2$
do not exhibit non-profinite second bounded cohomology.
$n \ge 2$
do not exhibit non-profinite second bounded cohomology.
Proof Let
![]() $\mathbf {G_0} = \mathbf {Sp_n}$
be the unique
$\mathbf {G_0} = \mathbf {Sp_n}$
be the unique
![]() $\mathbb {Q}$
-split simply-connected
$\mathbb {Q}$
-split simply-connected
![]() $\mathbb {Q}$
-group of type
$\mathbb {Q}$
-group of type
![]() $C_n$
. Then
$C_n$
. Then
![]() $\operatorname {Sym} \Delta = 1$
, so
$\operatorname {Sym} \Delta = 1$
, so
![]() $\operatorname {Aut} \mathbf {G_0} = \operatorname {Ad} \mathbf {G_0}$
and we have
$\operatorname {Aut} \mathbf {G_0} = \operatorname {Ad} \mathbf {G_0}$
and we have
![]() $Z(\mathbf {G_0}) = \mu _2$
. From the short exact sequence of
$Z(\mathbf {G_0}) = \mu _2$
. From the short exact sequence of
![]() $\operatorname {Gal}(\mathbb {Q})$
-groups
$\operatorname {Gal}(\mathbb {Q})$
-groups
we obtain a boundary map
![]() $\delta _K \colon H^1(K, \operatorname {Ad} \mathbf {G_0}) \rightarrow H^2(K, \mu _2)$
for any field extension
$\delta _K \colon H^1(K, \operatorname {Ad} \mathbf {G_0}) \rightarrow H^2(K, \mu _2)$
for any field extension
![]() $K/\mathbb {Q}$
. As we saw in [Reference Kammeyer and Spitler16, Section 5], the kernel of
$K/\mathbb {Q}$
. As we saw in [Reference Kammeyer and Spitler16, Section 5], the kernel of
![]() $\delta _{\mathbb {R}}$
consists of the class corresponding to the split form
$\delta _{\mathbb {R}}$
consists of the class corresponding to the split form
![]() $\operatorname {Sp}(n, \mathbb {R})$
only, while the other real forms of type
$\operatorname {Sp}(n, \mathbb {R})$
only, while the other real forms of type
![]() $C_n$
are the groups
$C_n$
are the groups
![]() $\operatorname {Sp}(p,q)$
with
$\operatorname {Sp}(p,q)$
with
![]() $p + q = n$
and they form precisely the fiber under
$p + q = n$
and they form precisely the fiber under
![]() $\delta _{\mathbb {R}}$
of the nontrivial element in
$\delta _{\mathbb {R}}$
of the nontrivial element in
![]() $H^2(\mathbb {R}, \mu _2) \cong \mathbb {Z} / 2 \mathbb {Z}$
. Let
$H^2(\mathbb {R}, \mu _2) \cong \mathbb {Z} / 2 \mathbb {Z}$
. Let
![]() $\alpha \in H^1(k, \operatorname {Ad} \mathbf {G_0})$
be the cohomology class corresponding to
$\alpha \in H^1(k, \operatorname {Ad} \mathbf {G_0})$
be the cohomology class corresponding to
![]() $\mathbf {G}$
, and let
$\mathbf {G}$
, and let
![]() $\beta \in H^1(l, \operatorname {Ad} \mathbf {G_0})$
be the cohomology class corresponding to
$\beta \in H^1(l, \operatorname {Ad} \mathbf {G_0})$
be the cohomology class corresponding to
![]() $\mathbf {H}$
. Then
$\mathbf {H}$
. Then
![]() $\delta _k(\alpha )$
and
$\delta _k(\alpha )$
and
![]() $\delta _l(\beta )$
map diagonally to corresponding elements under the isomorphism
$\delta _l(\beta )$
map diagonally to corresponding elements under the isomorphism
Indeed, this follows from the isomorphism
![]() $\eta $
for
$\eta $
for
![]() $u \nmid \infty $
. Additionally, we know that at infinite places
$u \nmid \infty $
. Additionally, we know that at infinite places
![]() $u \neq v$
and
$u \neq v$
and
![]() $u' \neq w$
, the groups
$u' \neq w$
, the groups
![]() $\mathbf {G}_{k_u}$
and
$\mathbf {G}_{k_u}$
and
![]() $\mathbf {H}_{l_{u'}}$
are anisotropic hence isomorphic to the unique anisotropic real form
$\mathbf {H}_{l_{u'}}$
are anisotropic hence isomorphic to the unique anisotropic real form
![]() $\operatorname {Sp}(n)$
of type
$\operatorname {Sp}(n)$
of type
![]() $C_n$
. The number field version of the Albert–Brauer–Hasse–Noether theorem (6) says that there is a short exact sequence
$C_n$
. The number field version of the Albert–Brauer–Hasse–Noether theorem (6) says that there is a short exact sequence
Since
![]() $\mathbf {G}_v \approx \operatorname {Sp}(n,\mathbb {R})$
is the real split form,
$\mathbf {G}_v \approx \operatorname {Sp}(n,\mathbb {R})$
is the real split form,
![]() $\alpha _v$
is trivial. Hence, so is
$\alpha _v$
is trivial. Hence, so is
![]() $\delta _{\mathbb {R}}(\alpha _v)$
and therefore also
$\delta _{\mathbb {R}}(\alpha _v)$
and therefore also
![]() $\delta _{\mathbb {R}}(\beta _w)$
by (12) and (13). So
$\delta _{\mathbb {R}}(\beta _w)$
by (12) and (13). So
![]() $\beta _w$
is trivial, too. This shows that
$\beta _w$
is trivial, too. This shows that
![]() $H \approx \operatorname {Sp}(n, \mathbb {R})$
is Hermitian.
$H \approx \operatorname {Sp}(n, \mathbb {R})$
is Hermitian.
Proposition 14 The groups
![]() $G \approx \operatorname {SO}^*(2n)$
with
$G \approx \operatorname {SO}^*(2n)$
with
![]() $n \ge 5$
do not exhibit non-profinite second bounded cohomology.
$n \ge 5$
do not exhibit non-profinite second bounded cohomology.
Proof In this case,
![]() $\mathbf {G}$
and
$\mathbf {G}$
and
![]() $\mathbf {H}$
have type
$\mathbf {H}$
have type
![]() $D_n$
, and it is more convenient to argue in terms of central simple algebras instead of Galois cohomology. Indeed, it is then well known by the work of Weil and Jacobson (see, for instance, [Reference Schoeneberg33, Theorem 4.5.10]) that there exist central simple algebras A and B over k and l, respectively, each endowed with an involution
$D_n$
, and it is more convenient to argue in terms of central simple algebras instead of Galois cohomology. Indeed, it is then well known by the work of Weil and Jacobson (see, for instance, [Reference Schoeneberg33, Theorem 4.5.10]) that there exist central simple algebras A and B over k and l, respectively, each endowed with an involution
![]() $\sigma $
of the first kind and of orthogonal type such that the skew symmetric Lie subalgebras of A and B consisting of the elements x satisfying
$\sigma $
of the first kind and of orthogonal type such that the skew symmetric Lie subalgebras of A and B consisting of the elements x satisfying
![]() $\sigma (x) = -x$
with commutator Lie bracket
$\sigma (x) = -x$
with commutator Lie bracket
![]() $[x,y] = xy - yx$
are k- and l-isomorphic to the Lie algebras
$[x,y] = xy - yx$
are k- and l-isomorphic to the Lie algebras
![]() $\mathfrak {g}$
of
$\mathfrak {g}$
of
![]() $\mathbf {G}$
and
$\mathbf {G}$
and
![]() $\mathfrak {h}$
of
$\mathfrak {h}$
of
![]() $\mathbf {H}$
, respectively. We have isomorphisms
$\mathbf {H}$
, respectively. We have isomorphisms
![]() $\mathfrak {g}_u \cong \mathfrak {h}_{u'}$
for all finite and infinite places u except possibly v. From [Reference Jacobson12, Chapter X, Theorem 12], we conclude that these extend uniquely to isomorphisms
$\mathfrak {g}_u \cong \mathfrak {h}_{u'}$
for all finite and infinite places u except possibly v. From [Reference Jacobson12, Chapter X, Theorem 12], we conclude that these extend uniquely to isomorphisms
![]() $A_u \cong B_{u'}$
which identify the involutions with one another. In particular,
$A_u \cong B_{u'}$
which identify the involutions with one another. In particular,
![]() $A_u$
and
$A_u$
and
![]() $B_{u'}$
have equal Brauer classes. But since
$B_{u'}$
have equal Brauer classes. But since
![]() $\mathfrak {g}_v \cong \mathfrak {so}^*(2n) = \mathfrak {so}(n, \mathbb {H})$
, it follows that
$\mathfrak {g}_v \cong \mathfrak {so}^*(2n) = \mathfrak {so}(n, \mathbb {H})$
, it follows that
![]() $A_v$
has a non-trivial Brauer class, so by the Albert–Brauer–Hasse–Noether theorem (13), the same is true for
$A_v$
has a non-trivial Brauer class, so by the Albert–Brauer–Hasse–Noether theorem (13), the same is true for
![]() $B_w$
. But all real forms of type
$B_w$
. But all real forms of type
![]() $D_n$
except
$D_n$
except
![]() $\mathfrak {so}^*(2n)$
are special orthogonal lie algebras of quadratic forms over
$\mathfrak {so}^*(2n)$
are special orthogonal lie algebras of quadratic forms over
![]() $\mathbb {R}$
, so the corresponding involutorial central simple algebra have trivial Brauer classes. Hence of necessity
$\mathbb {R}$
, so the corresponding involutorial central simple algebra have trivial Brauer classes. Hence of necessity
![]() $\mathfrak {h}_w \cong \mathfrak {so}^*(2n)$
as well. So H is isogenous to
$\mathfrak {h}_w \cong \mathfrak {so}^*(2n)$
as well. So H is isogenous to
![]() $\operatorname {SO}^*(2n)$
and hence Hermitian.
$\operatorname {SO}^*(2n)$
and hence Hermitian.
This leaves the group
![]() $G \approx \operatorname {SO}^0(5,2)$
as the only remaining case. The only higher-rank real twist of G up to isogeny is the group
$G \approx \operatorname {SO}^0(5,2)$
as the only remaining case. The only higher-rank real twist of G up to isogeny is the group
![]() $H \approx \operatorname {SO}^0(4,3)$
. However, this possibility can be excluded because the symmetric space defined by G is
$H \approx \operatorname {SO}^0(4,3)$
. However, this possibility can be excluded because the symmetric space defined by G is
![]() $10$
-dimensional, whereas the symmetric space defined by H is
$10$
-dimensional, whereas the symmetric space defined by H is
![]() $12$
-dimensional, and the dimension mod 4 is a profinite invariant by [Reference Kammeyer, Kionke, Raimbault and Sauer14, Theorem 2.1].
$12$
-dimensional, and the dimension mod 4 is a profinite invariant by [Reference Kammeyer, Kionke, Raimbault and Sauer14, Theorem 2.1].
Acknowledgment
We are indebted to Francesco Fournier-Facio, Ryan Spitler, and the referee for helpful discussions and suggestions.