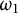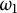Borel reducibility of equivalence relations on $\omega _1$

Abstract

The structure of Borel reducibility for equivalence relations on $\omega _1$ is determined.

1 Introduction

Let $X,Y$ be non-empty sets, and let $E,F$ be equivalence relations on $X,Y$ , respectively. A reduction of E to F is any function $f:X\to Y$ such that $\forall x,x'\in X\ (xEx'\Leftrightarrow f(x)Ff(x'))$ . Thus the existence of a reduction of E to F simply amounts to the inequality .

Therefore, one is generally interested in restricting the classes of reductions to be considered. These restricted classes are often defined by exploiting some extra structure of the sets they are defined on. A typical example is Borel reducibility: if $X,Y$ are topological spaces, then E Borel reduces to F, denoted $E\leqslant _BF$ , if there exists a Borel reduction $f:X\to Y$ of E to F. If $E\leqslant _BF\leqslant _BE$ , say that $E,F$ are Borel equivalent, denoted $E\sim _BF$ .

Borel reducibility has received much attention for equivalence relations defined on Polish spaces, and on such spaces, the structure of $\leqslant _B$ turns out to be very rich (see, for instance, [G2009] for a comprehensive introduction to the subject).

Much less is known concerning non-Polish spaces. This note focuses on one such space of interest in set theory: the ordinal $\omega _1$ endowed with the order topology. The structure of $\leqslant _B$ on equivalence relations on $\omega _1$ is much simpler than for Polish spaces, therefore allowing a complete description.

The paper is organized as follows: Section 2 recalls some basic set theoretic terminology and proves the facts on the Borel structure of $\omega _1$ that are needed later. In particular, Theorem 2.7 identifies the Borel functions $\omega _1\to \omega _1$ as those functions that are either constant on a club or the identity on a club, while Theorem 2.10 shows that the Cartesian product of Borel functions is Borel. This latter fact implies that Borel equivalence relations form an initial segment with respect to $\leqslant _B$ (Corollary 2.11). The analysis of $\leqslant _B$ on equivalence relations on $\omega _1$ is carried out in Section 3, leading to the complete description of its structure in terms of the characteristic triple of an equivalence relation (taking into account, how many classes the relation has of a given size) and the compatibility of the bistationary classes. Theorem 3.14 and Figure 1 summarize the results. Finally, Section 4 connects equivalence relations on $\omega _1$ with the better known realm of equivalence relations on Polish spaces.

Figure 1 The structure of Borel reducibility on $\omega _1$ .

Since by [GJK2008, Theorem 1.1], all ordinals $\alpha $ with $\omega _1\leqslant \alpha <\omega _12$ are Borel isomorphic, the structure of $\leqslant _B$ is the same on all such ordinals. This raises the following question.

Question What is the structure of $\leqslant _B$ on equivalence relations on $\alpha $ when $\alpha \ge \omega _12$ ?

2 Generalities on Borel sets and functions

The simplicity of $\leqslant _B$ on $\omega _1$ is due to the very rigid features of Borel subsets of $\omega _1$ and Borel functions $\omega _1\to \omega _1$ .

Recall that a subset of a regular uncountable cardinal is a club if it is closed in the ordinal topology and unbounded, it is stationary if it intersects every club, it is bistationary if both it and its complement are stationary. A collection of the fundamental properties of these sets can be found, for instance, in [J2002], and in [BL2020] for the specific case of $\omega _1$ . The following is a convenient terminology.

Definition 2.1 Let $A\subseteq \omega _1$ . Then:

• • A is thin if A is not stationary.

• • A is thick if its complement is thin, that is, if A contains a club.

Therefore, the subsets of $\omega _1$ are partitioned into three classes: thin, bistationary, and thick subsets. The union of countably many thin sets is thin, the intersection of countably many thick sets is thick.

The following known fact is used repeatedly in the sequel.

Theorem 2.2 A subset of $\omega _1$ is Borel if and only if it is either thin or thick; more precisely, every thin set is of the form $\bigcup _{n\in \mathbb N }E_n$ , where each $E_n$ is the intersection of an open and a closed set. Consequently, a function $f:\omega _1\to \omega _1$ is Borel if and only if the preimage under f of any thick set (equivalently, of any thin set) is either thin or thick.

Proof See [BL2020, Proposition 4] and its proof.

See theorem 2.7 for a characterization of Borel functions.

The proof of the existence of bistationary subsets of $\omega _1$ uses the axiom of choice (see [Ru1957]). With the same idea, the following strengthening can be established.

Lemma 2.3 Let $ \mathcal F $ be a partition of a thick set C into non-thick sets. Then there exists $ \mathcal G \subseteq \mathcal F $ such that $\bigcup \mathcal G $ is bistationary.

Proof Notice that it can be assumed that $C=\omega _1$ . Indeed, otherwise $ \mathcal F \cup \{\omega _1\setminus C\} $ is a partition of $\omega _1$ into non-thick sets. Since $\omega _1\setminus C$ is thin, if $ \mathcal G \subseteq \mathcal F \cup \{\omega _1\setminus C\} $ is such that $\bigcup \mathcal G $ is bistationary, then $\bigcup ( \mathcal G \setminus \{\omega _1\setminus C\} )$ is bistationary as well.

It can also be assumed that all members of $ \mathcal F $ are thin, otherwise $ \mathcal G =\{ A\} $ for A non-thin works because every element of $ \mathcal F $ is assumed to be non-thick; thus such an A is bistationary. In particular, $ \mathrm {{card}} ( \mathcal F )=\aleph _1$ , so let $ \mathcal F =\{ A_{\alpha }\}_{\alpha \in \omega _1}$ .

Now, toward contradiction assume that for every $ \mathcal G \subseteq \mathcal F $ ,

(2.1) $$ \begin{align} \text{either} \quad\bigcup \mathcal G \text{ is thick} \quad \text{or} \quad\omega_1\setminus\bigcup \mathcal G =\bigcup ( \mathcal F \setminus \mathcal G ) \text{ is thick.} \end{align} $$

Let $g:\omega _1\to \mathbb R $ be an injection. For every $n\in \mathbb N $ , let $ \mathcal J (n)=\{ B_{nm}\}_{m\in \mathbb N }$ be a partition of $ \mathbb R $ into subsets of diameter less than $ \frac 1{n+1} $ .

Claim 2.4 For every $n,$ there exists $m_n$ such that $D_n=\bigcup _{\alpha \in g^{-1}(B_{nm_n})}A_{\alpha }$ is thick.

Proof of the claim

Otherwise, by (2.1), for every $m,$ the set $\bigcup _{\alpha \in \omega _1\setminus g^{-1}(B_{nm})}A_{\alpha }$ would be thick, contradicting $\bigcap _{m\in \mathbb N }\bigcup _{\alpha \in \omega _1\setminus g^{-1}(B_{nm})}A_{\alpha }=\emptyset $ .

Let $D=\bigcap _{n\in \mathbb N }D_n=\bigcup _{\alpha \in \bigcap _{n\in \mathbb N }g^{-1}(B_{nm_n})}A_{\alpha }$ , so that D is thick, implying that $\bigcap _{n\in \mathbb N }g^{-1}(B_{nm_n})$ has more than one element. Let $\alpha ,\beta \in \bigcap _{n\in \mathbb N }g^{-1}(B_{nm_n})$ with $\alpha \ne \beta $ , so that $g(\alpha )\ne g(\beta )$ ; on the other hand, $\alpha ,\beta \in \bigcap _{n\in \mathbb N }g^{-1}(B_{nm_n})$ implies that $|g(\alpha )-g(\beta )|< \frac 1{n+1} $ for every $n\in \mathbb N $ , reaching a contradiction.

Lemma 2.5 Let $ \mathcal F $ be a family of pairwise disjoint thin sets. Then there exists a club C such that $\forall A\in \mathcal F \ \mathrm {{card}} (C\cap A)\leqslant 1$ .

Proof It can be assumed that no member of $ \mathcal F $ is empty and that $ \mathrm {{card}} ( \mathcal F )=\aleph _1$ . Let $ \mathcal F =\{ A_{\alpha }\}_{\alpha \in \omega _1}$ such that $\alpha <\beta \Rightarrow \min A_{\alpha }<\min A_{\beta }$ ; in particular,

(2.2) $$ \begin{align} \forall\alpha\in\omega_1\ \alpha\leqslant\min A_{\alpha }. \end{align} $$

For every $\alpha \in \omega _1$ , let $C_{\alpha }$ be a club such that $C_{\alpha }\cap \bigcup _{\beta \leqslant \alpha }A_{\beta }=\emptyset $ , and consider the diagonal intersection $C=\triangle _{\alpha \in \omega _1}C_{\alpha }=\{\beta \in \omega _1\mid \beta \in \bigcap _{\alpha <\beta }C_{\alpha }\} $ , which is a club by [J2002, Lemma 8.4]. If $\beta \in C$ , then $\beta \notin \bigcup _{\alpha <\beta }A_{\alpha }$ by construction of C, and $\beta \notin \bigcup _{\alpha>\beta }A_{\alpha }$ by (2.2); in other words, any $\beta \in C$ cannot belong to any $A_{\alpha }$ but $A_{\beta }$ . This establishes the lemma.

Lemma 2.6 Let $f:\omega _1\to \omega _1$ be Borel and assume that $f[C]$ is thin for some thick set C. Then there exists $\beta \in f[C]$ such that $f^{-1}(\{\beta \} )$ is thick.

Proof If the conclusion did not hold, $\{ f^{-1}(\{\beta \} )\cap C\}_{\beta \in f[C]}$ would be a partition of C into thin sets, by Theorem 2.2. By Lemma 2.3, there exists $I\subseteq f[C]$ such that $\bigcup _{\beta \in I}f^{-1}(\{\beta \} )\cap C=f^{-1}(I)\cap C$ is bistationary. Since I is thin, this contradicts f being Borel, again by Theorem 2.2.

The following theorem imposes severe restrictions to Borel functions.

Theorem 2.7 Let $f:\omega _1\to \omega _1$ . Then the following are equivalent:

1. (1) f is Borel.

2. (2) There exists a thick set C such that $f_{|_C}$ is continuous.

3. (3) There exists a thick set C such that either f is constant on C or $\forall \alpha \in C\ f(\alpha )=\alpha $ .

Proof $(1)\Rightarrow (3)$ . Assume that f is Borel. Let $S=\{\alpha \in \omega _1\mid f(\alpha )<\alpha \} $ .

If S is stationary, by Fodor’s theorem, let $\beta $ be such that $C=f^{-1}(\{\beta \} )$ is stationary. Actually, C is thick: otherwise, it would be bistationary, contradicting the Borelness of f. So in this case, the conclusion is achieved.

Assume now that S is thin, and let F be a club disjoint from S. In particular, $\forall \alpha \in F\ \alpha \leqslant f(\alpha )$ . Define an increasing, continuous at limits, sequence $\{\gamma _{\rho }\}_{\rho \in \omega _1}$ of elements of F as follows:

$$ \begin{align*} \begin{array}{ll} \gamma_0=\min F, \\ \gamma_{\rho }=\min\{\alpha\in F\mid\forall\xi <\rho\ f(\gamma_{\xi })<\alpha\} , & \text{for } \rho>0. \end{array} \end{align*} $$

Let $L=\{\gamma _{\rho }\}_{\rho \in \omega _1}$ , so L is a club and $f_{|_L}$ is injective. If $C=\{\alpha \in L\mid f(\alpha )=\alpha \} $ is thick, then it has the desired properties, so toward contradiction assume otherwise: this means that either C is thin or it is bistationary. Let $G=\{\alpha \in L\mid \alpha <f(\alpha )\} =L\setminus C$ .

Claim 2.8 $f[G]$ is thin.

Proof of the claim

In fact, $f[G]$ does not contain any of its limit points. Let $\{\rho _n\}_{n\in \mathbb N }$ be any increasing sequence of elements of $\omega _1$ such that $\forall n\in \mathbb N \ \gamma _{\rho _n}<f(\gamma _{\rho _n})$ , and let $\lambda =\sup \{ f(\gamma _{\rho _n})\}_{n\in \mathbb N } =\sup \{\gamma _{\rho _n}\}_{n\in \mathbb N }\in L$ . Then $\lambda \leqslant f(\lambda )$ . If $\lambda =f(\lambda ),$ then ${\lambda \notin G}$ , so $\lambda \notin f[G]$ by the injectivity of $f_{|_L}$ ; if $\lambda <f(\lambda ),$ then $\lambda \notin f[G]$ by the construction of L.

If C were thin, then G would be thick. Thus, by the claim and Lemma 2.6, function f would be constant on a thick set, which is impossible as $f_{|_G}$ is injective.

If C were bistationary, G would be bistationary too. Now, note that $f^{-1}(f[G])\cap L=G$ by the injectivity of $f_{|_L}$ , but this is impossible, as $f[G]$ is Borel by the claim, while G is not.

$(3)\Rightarrow (2)$ is immediate.

$(2)\Rightarrow (1)$ . Let $C'$ be a club included in C. By [A2018, Theorem 4.1], either f is constant, say of value $\beta $ , on a final segment of $C'$ , so on a thick set, or the set of fixed points of $f_{|_{C'}}$ is cofinal. In the former case, given any $B\subseteq \omega _1$ , one has that $f^{-1}(B)$ is either thin or thick, according to whether $\beta \notin B$ or $\beta \in B$ ; so f is Borel by Theorem 2.2. In the latter case, by the continuity of $f_{|_{C'}}$ , the set F of fixed points of $f_{|_{C'}}$ is also closed, therefore a thick set. Let then B be a thick set. Thus $B\cap F$ is thick as well. It follows that $f^{-1}(B)\supseteq f^{-1}(B\cap F)\supseteq B\cap F$ , so $f^{-1}(B)$ is a thick set. Thus f is Borel by Theorem 2.2 again.

Therefore, even a very simple function like the successor function $f:\omega _1\to \omega _1$ , defined by $f(\alpha )=\alpha +1$ , is not Borel, since it does not satisfy the condition of Theorem 2.7(3).

For $S\subseteq \omega _1\times \omega _1$ and $\xi \in \omega _1$ denote $S_{\xi }=\{\rho \in \omega _1\mid (\xi ,\rho )\in S\} $ the vertical section and $S^{\xi }=\{\rho \in \omega _1\mid (\rho ,\xi )\in S\} $ the horizontal section of S corresponding to $\xi $ .

Lemma 2.9 Let A be a thin set, and let $F\subseteq A\times \omega _1$ be a set all of whose vertical sections are Borel. Then F is Borel.

Similarly, if $F\subseteq \omega _1\times A$ is a set all of whose horizontal sections are Borel.

Proof The proof is an extension of the argument of [BL2020, Proposition 4]. Assume that $F\ne \emptyset $ , and let $A'=\pi _1(F),$ where $\pi _1$ denotes the first projection.

Suppose first that all vertical sections of F are closed. Let H be a club such that $A'\cap H=\emptyset $ , and let $ \mathcal D $ be the partition of $\omega _1\setminus H$ into maximal convex open sets, so that each member of $ \mathcal D $ is countable. Let $ \mathcal D'=\{ D\in \mathcal D \mid A'\cap D\ne \emptyset \} $ ; then $A'=\bigcup _{D\in \mathcal D'}(A'\cap D)$ . For every $D\in \mathcal D'$ , let $A'\cap D=\{\xi _{Dn}\}_{n\in \mathbb N }$ , allowing repetitions if $A'\cap D$ is finite. For every $n\in \mathbb N $ , let $F(n)=\bigcup _{D\in \mathcal D'}(\{\xi _{Dn}\}\times F_{\xi _{Dn}})$ and note that $F(n)= \overline {F(n)} \cap ((\omega _1\setminus H)\times \omega _1)$ , so $F(n)$ is Borel. Finally, $F=\bigcup _{n\in \mathbb N }F(n)$ is Borel.

By taking in succession complements in $A\times \omega _1$ , intersections, and countable unions, the statement holds for F having sections that are respectively open, intersections of an open and a closed set, countable unions of intersections of an open and a closed set, that is general thin sets. If the non-empty vertical sections of F are thick, apply the statement to $(A'\times \omega _1)\setminus F$ , to get the statement for F. To conclude the proof, observe that every set with Borel vertical sections is the union of a set with thin vertical sections and a set with non-empty vertical sections that are thick.

Theorem 2.10 Let $f,g:\omega _1\to \omega _1$ be Borel. Then $f\times g:\omega _1\times \omega _1\to \omega _1\times \omega _1$ is Borel.

Proof By Theorem 2.7, there exists a club C such that one of the following four cases holds:

1. (i) $f_{|_C},g_{|_C}$ are constant, say with values $\gamma ,\delta $ , respectively.

2. (ii) $\forall \alpha \in C\ f(\alpha )=g(\alpha )=\alpha. $

3. (iii) $f_{|_C}$ is constant, say with value $\gamma $ , and $\forall \alpha \in C\ g(\alpha )=\alpha. $

4. (iv) $\forall \alpha \in C\ f(\alpha )=\alpha $ and $g_{|_C}$ is constant.

Let B be a Borel subset of $\omega _1\times \omega _1$ , in order to prove that $(f\times g)^{-1}(B)$ is Borel. Note that

$$ \begin{align*} (f\times g)^{-1}(B)& = \\ & =((f\times g)^{-1}(B)\cap C^2)\cup ((f\times g)^{-1}(B)\cap ((\omega_1\setminus C)\times C))\cup \\ & \cup ((f\times g)^{-1}(B)\cap (C\times (\omega_1\setminus C)))\cup ((f\times g)^{-1}(B)\cap (\omega_1\setminus C)^2). \end{align*} $$

Every subset of $\omega _1\setminus C$ is Borel, so every subset of $(\omega _1\setminus C)^2$ is Borel by Lemma 2.9. Thus, it remains to prove that the other three terms in the union are Borel.

Case (i).

• •

  $$\begin{align*}(f\times g)^{-1}(B)\cap C^2= \begin{cases} \emptyset, & \text{if } (\gamma ,\delta )\notin B, \\ C^2, & \text{if } (\gamma ,\delta )\in B, \end{cases} \end{align*}$$
  so $(f\times g)^{-1}(B)\cap C^2$ is Borel.

• •

  $$ \begin{align*} & (f\times g)^{-1}(B)\cap ((\omega_1\setminus C)\times C)= \\ & =\{ (\alpha ,\beta)\in (\omega_1\setminus C)\times C\mid (f(\alpha ),\delta )\in B\} = \\ & =\{ (\alpha ,\beta )\in (\omega_1\setminus C)\times C\mid f(\alpha )\in B^{\delta }\} =(f^{-1}(B^{\delta })\setminus C)\times C \end{align*} $$
  is Borel. Similarly, for $(f\times g)^{-1}(B)\cap (C\times (\omega _1\setminus C))$ .

Case (ii).

• • $(f\times g)^{-1}(B)\cap C^2=B\cap C^2$ is Borel.

• •

  (2.3) $$ \begin{align} \begin{array}{l} (f\times g)^{-1}(B)\cap ((\omega_1\setminus C)\times C)= \\ =\{ (\alpha ,\beta)\in (\omega_1\setminus C)\times C\mid (f(\alpha ),\beta )\in B\} = \\ =\{ (\alpha ,\beta )\in (\omega_1\setminus C)\times C\mid\beta\in B_{f(\alpha )}\} = \\ =\bigcup_{\alpha\in\omega_1\setminus C}(\{\alpha\}\times (B_{f(\alpha )}\cap C)) \end{array} \end{align} $$
  is Borel by Lemma 2.9. Similarly, for $(f\times g)^{-1}(B)\cap (C\times (\omega _1\setminus C))$ .

Case (iii).

• •

  $$ \begin{align*} & (f\times g)^{-1}(B)\cap C^2=\{ (\alpha ,\beta )\in C^2\mid (\gamma ,\beta )\in B\} = \\ & =\{ (\alpha ,\beta )\in C^2\mid\beta\in B_{\gamma }\} =C\times (B_{\gamma }\cap C) \end{align*} $$
  is Borel.

• • For $(f\times g)^{-1}(B)\cap ((\omega _1\setminus C)\times C),$ the computation is the same as in (2.3).

• •

  $$ \begin{align*} & (f\times g)^{-1}(B)\cap (C\times (\omega_1\setminus C))=\{ (\alpha ,\beta )\in C\times (\omega_1\setminus C)\mid (\gamma ,g(\beta ))\in B\} = \\ & =\{ (\alpha ,\beta )\in C\times (\omega_1\setminus C)\mid g(\beta )\in B^{\gamma }\} =C\times (g^{-1}(B^{\gamma })\setminus C) \end{align*} $$
  is Borel.

Case (iv). This is similar to case (iii).

Corollary 2.11 If $E,F$ are equivalence relations on $\omega _1$ with F Borel and $E\leqslant _BF$ , then E is Borel.

Proof Let f be a Borel reduction of E to F. Then $E=(f\times f)^{-1}(F)$ . Apply Theorem 2.10.

3 Equivalence relations on $\omega _1$

A key tool to compare equivalence relations on $\omega _1$ consists in counting their classes according to their size.

Definition 3.1 For E an equivalence relation on $\omega _1$ , let the characteristic triple of E be the triple of cardinal numbers $K=(\kappa _0^E,\kappa _1^E,\kappa _2^E)$ where:

$$ \begin{align*} & \kappa_0^E \text{ is the number of thick equivalence classes of } E. \\ &\qquad\qquad \kappa_1^E \text{ is the number of bistationary equivalence classes of } E. \\ &\qquad\qquad\qquad\quad \kappa_2^E \text{ is the number of thin equivalence classes of } E. \end{align*} $$

Let $ \mathcal E (\kappa _0,\kappa _1,\kappa _2)$ be the set of equivalence relations of characteristic triple $(\kappa _0,\kappa _1,\kappa _2)$ .

Note that:

(3.1) $$ \begin{align} \kappa_0^E\in\{ 0,1\} ,\quad 0\leqslant\kappa_1^E\leqslant\aleph_1,\quad 0\leqslant\kappa_2^E\leqslant\aleph_1, \end{align} $$

moreover, by the definition of stationarity and the fact that the union of countably many thin sets is thin:

1. (i) If $\kappa _0^E=1$ then $\kappa _1^E=0.$

2. (ii) If $\kappa _0^E=\kappa _1^E=0$ , then $\kappa _2^E=\aleph _1.$

3. (iii) If $\kappa _1^E=1$ , then $\kappa _2^E=\aleph _1.$

Notice that (3.1) and the conditions (i–iii) above are the only constraints on the characteristic triple of an equivalence relation on $\omega _1$ : if $K=(\kappa _0,\kappa _1,\kappa _2)$ satisfies such conditions, there exists a partition of $\omega _1$ with $\kappa _0$ thick elements, $\kappa _1$ bistationary elements, and $\kappa _2$ thin elements.

Definition 3.2 A triple $K=(\kappa _0,\kappa _1,\kappa _2)$ of cardinals satisfying (3.1) and the conditions (i–iii) above is a legitimate triple.

In other words, $(\kappa _0,\kappa _1,\kappa _2)$ is a legitimate triple if and only if $ \mathcal E (\kappa _0,\kappa _1,\kappa _2)\ne \emptyset $ . The legitimate triples are represented as labels of the nodes in Figure 1.

3.1 Equivalence relations with a thick class

This section deals with equivalence relations whose characteristic triple is $(1,0,\kappa ),$ where $0\leqslant \kappa \leqslant \aleph _1$ . It turns out that such relations form an initial segment with respect to $\leqslant _B$ , and they Borel reduce to any equivalence relation with at least the same number of classes. Consequently, they are Borel by Corollary 2.11, since they Borel reduce to the equality relation which is closed.

Proposition 3.3 Let $E,F$ be equivalence relations on $\omega _1$ such that E has a thick equivalence class. Then .

Proof The implication from left to right holds for any reduction.

As for the opposite implication, let $\{ A_{\gamma }\}_{\gamma },\{ B_{\gamma }\}_{\gamma }$ be enumerations of the equivalence classes of $E,F$ , respectively. Let $f:\omega _1\to \omega _1$ be defined by letting $f(\alpha )=\min B_{\gamma }$ if $\alpha \in A_{\gamma }$ . Being constant on a thick equivalence class, f is Borel by Theorem 2.7; moreover, it reduces E to F.

Proposition 3.4 Let $E,F$ be equivalence relations on $\omega _1$ . Assume that E has a thick equivalence class and $F\leqslant _BE$ . Then F has a thick equivalence class.

Proof Deny. Let $f:\omega _1\to \omega _1$ be a Borel reduction of F to E. Then f is not constant on a thick set, since F does not have thick equivalence classes. Thus, by Theorem 2.7, there exists a thick set C such that $\forall \alpha \in C\ f(\alpha )=\alpha $ . Let A be the thick equivalence class of E, so that $C\cap A$ is thick; therefore, there exist F-inequivalent elements in $C\cap A$ that are sent by f to E-equivalent elements (namely, themselves), which is a contradiction.

Corollary 3.5 Let $E,F$ be equivalence relations on $\omega _1$ . Assume that E has a thick equivalence class and no equivalence class of F is thick. Then

3.2 Equivalence relations of all whose classes are thin

Corollary 3.5 implies that all equivalence relations with a thick class Borel reduce to the equivalence relations whose classes are thin, like the equality relation. Actually, up to $\sim _B$ , there is just one such equivalence relation. Thus, by Corollary 2.11, all such relations are Borel.

Proposition 3.6 Let $E,F$ be equivalence relations on $\omega _1$ all of whose equivalence classes are thin. Then $E\sim _BF$ .

Proof Using Lemma 2.5, let $C_E$ be a club intersecting every equivalence class of E in at most one point, and let $C_F$ be a club intersecting every equivalence class of F in at most one point. Let $C=C_E\cap C_F$ , and let $C'\subseteq C$ be a club such that $ \mathrm {{card}} (C\setminus C')=\aleph _1$ – for instance, let $C'$ be the set of limit points of C. In particular, $C'$ misses $\aleph _1$ equivalence classes of E and $\aleph _1$ equivalence classes of F: let $\{ A_{\gamma }\}_{\gamma \in \omega _1},\{ B_{\gamma }\}_{\gamma \in \omega _1}$ be enumerations of such classes.

Let $f:\omega _1\to \omega _1$ be defined by

$$\begin{align*}f(\alpha )= \begin{cases} \beta, & \text{if } \alpha E\beta\in C', \\ \min B_{\gamma }, & \text{if } \alpha\in A_{\gamma }. \end{cases} \end{align*}$$

Then f is Borel by Theorem 2.7 and witnesses $E\leqslant _BF$ .

Similarly, $F\leqslant _BE$ .

3.3 Equivalence relations with some bistationary classes

This section focuses on equivalence relations having some bistationary classes; due to the presence of non-Borel classes, such equivalence relations are not Borel.

Definition 3.7 Let $E,F$ be equivalence relations on $\omega _1$ such that $\kappa _1^E=\kappa _1^F$ . Let $\{ A_{\alpha }\}_{\alpha <\kappa _1^E},\{ B_{\alpha }\}_{\alpha <\kappa _1^E}$ be enumerations of the bistationary classes of $E,F$ , respectively. Say that such enumerations are compatible if there exists a club C such that

(3.2) $$ \begin{align} \forall\alpha <\kappa_1^E\ A_{\alpha }\cap C=B_{\alpha }\cap C. \end{align} $$

The club C is a witness of compatibility for $E,F$ .

Note that when (3.2) holds, every symmetric difference $A_{\alpha }\triangle B_{\alpha }$ is a thin set.

Proposition 3.8 Let $E,F$ be equivalence relations on $\omega _1$ such that $E\leqslant _BF$ . Assume that $\kappa _1^E>0$ . Then $E,F$ admit compatible enumerations of their bistationary equivalence classes. In particular, $\kappa _1^E=\kappa _1^F$ . Moreover, $\kappa _2^E\leqslant \kappa _2^F$ .

Proof Let f be a Borel reduction of E to F. Since $\kappa _0^E=0$ , function f cannot be constant on a thick set, so by Theorem 2.7, let C be a club such that $\forall \alpha \in C\ f(\alpha )=\alpha $ . Then, for every bistationary equivalence class A of E, the set $A\cap C$ is bistationary and the elements of $f[A\cap C]=A\cap C$ are pairwise F-equivalent, so that $A\cap C$ is included in a single stationary F-class. Similarly, for every stationary equivalence class B of F, it holds that the stationary set $B\cap C$ is included in a single E-class, so $B\cap C$ is actually bistationary and B is bistationary as well. This shows that the bistationary equivalence classes of E and the bistationary equivalence classes of F can be enumerated compatibly, say as $\{ A_{\alpha }\}_{\alpha <\kappa _1^E},\{ B_{\alpha }\}_{\alpha <\kappa _1^E}$ , respectively, with C as witness of compatibility.

The last assertion follows from $\kappa _0^E=\kappa _0^F=0$ and the fact that f sends the elements of each $A_{\alpha }$ to elements in the corresponding $B_{\alpha }$ ; therefore, f sends elements belonging to thin classes of E to elements belonging to thin classes of F.

The converse of Proposition 3.8 holds as well.

Proposition 3.9 Let $E,F$ be equivalence relations such that $\kappa _1^E=\kappa _1^F>0$ and $\kappa _2^E\leqslant \kappa _2^F$ . Suppose that $E,F$ admit compatible enumerations of their bistationary equivalence classes. Then $E\leqslant _BF$ .

Proof Let $\{ A_{\alpha }\}_{\alpha <\kappa _1^E},\{ B_{\alpha }\}_{\alpha <\kappa _1^E}$ be compatible enumerations of the bistationary equivalence classes of $E,F$ , respectively. Let C be a witness of compatibility.

Assume first that $\bigcup _{\alpha <\kappa _1^E}A_{\alpha }$ is thick, and let $C'$ be a club with $C'\subseteq \bigcup _{\alpha <\kappa _1^E}A_{\alpha }$ . Define $f:\omega _1\to \omega _1$ such that:

• • If $\xi \in C\cap C'$ , then $f(\xi )=\xi $ .

• • If $\xi \in A_{\alpha }\setminus (C\cap C')$ , then $f(\xi )=\min B_{\alpha }$ .

• • f induces a reduction of the restriction of E to $\omega _1\setminus \bigcup _{\alpha <\kappa _1^E}A_{\alpha }$ to the restriction of F to $\omega _1\setminus \bigcup _{\alpha <\kappa _1^E}B_{\alpha }$ . This can be done as $\kappa _2^E\leqslant \kappa _2^F$ .

Then f is Borel by Theorem 2.7 and reduces E to F.

Assume now that $\bigcup _{\alpha <\kappa _1^E}A_{\alpha }$ is bistationary.

Claim 3.10 $\bigcup _{\alpha <\kappa _1^E}B_{\alpha }$ is bistationary.

Proof of the claim

If $\bigcup _{\alpha <\kappa _1^E}B_{\alpha }$ were thick, let $C_0$ be a club with $C_0\subseteq \bigcup _{\alpha <\kappa _1^E}B_{\alpha }$ . Then $C\cap C_0$ is also a witness of compatibility for $E,F$ and $C\cap C_0\subseteq \bigcup _{\alpha <\kappa _1^E}A_{\alpha }$ , so $\bigcup _{\alpha <\kappa _1^E}A_{\alpha }$ would be thick.

From the assumption and the claim, it follows also that $\kappa _2^E=\kappa _2^F=\aleph _1$ . By Lemma 2.5, let $C'$ be a club intersecting in at most one point every thin equivalence class of E. Similarly, let $C"$ be a club intersecting in at most one point every thin equivalence class of F. By [KT2006, Chapter 20, Problem 25], let $ \mathcal F $ be a family of cardinality $\aleph _1$ of thin equivalence classes of F such that $\bigcup \mathcal F $ is thin, and let $C"'$ be a club disjoint from $\bigcup \mathcal F $ . Set $D=C\cap C'\cap C"\cap C"'$ .

Define $f:\omega _1\to \omega _1$ such that:

• • If $\xi \in D$ , then $f(\xi )=\xi $ .

• • If $\xi \notin D$ but there exists a least $\zeta $ such that $\xi E\zeta \in D$ then $f(\xi )=\zeta $ .

• • f induces a reduction of the restriction of E to $\{\xi \in \omega _1\mid [\xi ]_E\cap D=\emptyset \} $ to the restriction of F to $\{\xi \in \omega _1\mid [\xi ]_F\cap D=\emptyset \} $ . This is possible by the choice of $C"'$ .

Then f is Borel by Theorem 2.7 and witnesses $E\leqslant _BF$ .

Corollary 3.11 If $E,F$ are equivalence relations on $\omega _1$ having the same characteristic triple $(0,\kappa _1,\kappa _2)$ with $\kappa _1>0$ , then $E\leqslant _BF\Leftrightarrow E\sim _BF$ .

Proof Assume $E\leqslant _BF$ . By Proposition 3.8, $E,F$ admit compatible enumerations of their bistationary equivalence classes. Therefore, by Proposition 3.9, with the role of $E,F$ switched, $F\leqslant _BE$ .

Thus, up to $\sim _B$ , the equivalence relations with at least one bistationary class having a given characteristic triple form an antichain. This antichain is as big as it can be.

Proposition 3.12 Let $K=(0,\kappa _1,\kappa _2)$ be a legitimate triple with $\kappa _1>0$ . Then there is a $\leqslant _B$ -antichain of cardinality $2^{\aleph _1}$ of equivalence relations having K as characteristic triple.

Proof Let $\{ S_{\alpha }\}_{\alpha \in \omega _1}$ be a partition of $\omega _1$ into bistationary sets. This exists by [BL2020, Corollary 8].

To deal with the case $\kappa _1=1,\kappa _2=\aleph _1$ , for every non-empty, proper subset I of $\omega _1,$ let $E_I$ be the equivalence relation having $\bigcup _{\alpha \in I }S_{\alpha }$ as one equivalence class, all other equivalence classes being singletons. Then characteristic triple of $E_I$ is $(0,1,\aleph _1)$ and $I\ne J\Rightarrow E_I\nleqslant _BE_J$ by Proposition 3.8.

For the case $\kappa _1>1$ , let

$$\begin{align*}S^{\prime}_{\alpha }= \begin{cases} S_{\alpha }\setminus\{\min S_{\alpha }\}, & \text{if } \alpha <\kappa_2, \\ S_{\alpha }, & \text{if } \kappa_2\le\alpha. \end{cases} \end{align*}$$

Then each $S^{\prime }{\alpha }$ is bistationary as well. For every partition $ \mathcal P $ of $\omega _1$ into $\kappa _1$ subsets, let $E_{ \mathcal P }$ be the equivalence relations whose classes are all bistationary subsets $\bigcup _{\alpha \in P}S^{\prime }_{\alpha }$ for $P\in \mathcal P $ and all singletons $\{\min S_{\alpha }\} $ for $\alpha <\kappa _2$ . Then the characteristic triple of each $E_{ \mathcal P }$ is $(0,\kappa _1,\kappa _2)$ and $ \mathcal P \ne \mathcal Q\Rightarrow E_{ \mathcal P }\nleqslant _BE_{ \mathcal Q }$ by Proposition 3.8 again.

If E is an equivalence relation on $\omega _1$ denote by $[E]_{\sim }$ the $\sim _B$ -class of E.

Proposition 3.13 Let $(0,\kappa _1,\kappa _2),(0,\kappa _1,\kappa ^{\prime }_2)$ be legitimate triples, with $\kappa _1>0$ and $\kappa _2<\kappa ^{\prime }_2$ . Setting $\varphi ([E]_{\sim })=[F]_{\sim }\Leftrightarrow E\leqslant _BF$ defines an injection . The range of $\varphi $ is the set of all such that the union of the thin equivalence classes of F is thin. In particular, $\varphi $ is surjective if and only if $\kappa ^{\prime }_2\leqslant \aleph _0$ .

Proof First, notice that for every $E\in \mathcal E (0,\kappa _1,\kappa _2),$ there exists $F\in \mathcal E (0,\kappa _1,\kappa ^{\prime }_2)$ such that $E\leqslant _BF$ . Indeed, let A be a bistationary equivalence class of E, and let $\kappa $ be such that $\kappa _2+\kappa =\kappa ^{\prime }_2$ . By [KT2006, Chapter 20, Problem 25], let $B\subseteq A$ such that B is thin and $ \mathrm {{card}} (B)=\kappa $ . Let F be the equivalence relation whose equivalence classes are $A\setminus B$ , all equivalence classes of E distinct from A, and all singleton subsets of B. Then the characteristic triple of F is $(0,\kappa _1,\kappa ^{\prime }_2)$ and $E\leqslant _BF$ by Proposition 3.9, since any club disjoint from B is a witness of compatibility for $E,F$ .

Function $\varphi $ is well defined and injective by Propositions 3.8 and 3.9.

Assume that the union of the thin equivalence classes of $F\in \mathcal E (0,\kappa _1,\kappa ^{\prime }_2)$ is thin, and let C be a club disjoint from such a union. Let E be the equivalence relation having the same bistationary equivalence classes of F and $\kappa _2$ thin equivalence classes. Then $E\in \mathcal E (0,\kappa _1,\kappa _2)$ and $E\leqslant _BF$ by Proposition 3.9. Thus $[F]_{\sim }$ belongs to the range of $\varphi $ .

Assume instead that the union of the thin equivalence classes of $F\in \mathcal E (0,\kappa _1,\kappa ^{\prime }_2)$ is stationary, so that in particular $\kappa ^{\prime }_2=\aleph _1$ . Toward contradiction, suppose that $E\in \mathcal E (0,\kappa _1,\kappa _2)$ and that there exists a Borel reduction f of E to F. By Theorem 2.7, let C be a club such that $\forall \alpha \in C\ f(\alpha )=\alpha $ and note that C intersects $\aleph _1$ thin equivalence classes of F, each of such intersections being a thin set. Therefore, E must have $\aleph _1$ equivalence classes intersecting C in a thin set, therefore, E has $\aleph _1$ thin equivalence classes, contradicting $\kappa _2<\kappa ^{\prime }_2=\aleph _1$ . So in this case, $[F]_{\sim }$ is not in the range of $\varphi $ .

3.4 Summarizing the results

The following theorem collects the results of the preceding sections characterizing Borel reducibility of equivalence relations on $\omega _1$ .

Theorem 3.14 Let $E,F$ be equivalence relations on $\omega _1$ . Then $E\leqslant _BF$ if and only if one of the following conditions holds:

1. (i) $\kappa _0^E=1$ and

2. (ii) $\kappa _0^E=\kappa _0^F=\kappa _1^E=\kappa _1^F=0$ and $\kappa _2^E=\kappa _2^F=\aleph _1$ .

3. (iii) $\kappa _0^E=\kappa _0^F=0,\kappa _1^E=\kappa _1^F>0$ , relations $E,F$ admit compatible enumerations of their bistationary classes, and $\kappa _2^E\leqslant \kappa _2^F$ .

This structure is also represented in Figure 1, where the triples labeling each node are the characteristic triples of the equivalence relations in that node.

• • Unboxed nodes contain just one equivalence relation up to $\sim _B$ . These have characteristic triple of the form $(1,0,\kappa _2)$ or $(0,0,\aleph _1)$ and are the Borel equivalence relations on $\omega _1$ .

• • Boxed nodes, corresponding to characteristic triples of the form $(0,\kappa _1,\kappa _2)$ with $\kappa _1\geqslant 1$ , represent antichains of size $2^{\aleph _1}$ .

• • Solid arrows mean that every equivalence relation at the tail of the arrow Borel reduces to every equivalence relation at the head of the arrow.

• • Dashed arrows, between nodes labeled $(0,\kappa _1,\kappa _2)$ and $(0,\kappa _1,\kappa ^{\prime }2)$ with $\kappa _2<\kappa ^{\prime }_2\le \aleph _0$ , mean that $\leqslant _B$ is a bijective correspondence between the $\sim _B$ -classes of equivalence relations with such characteristic triples.

• • Dashed and dotted arrows, between nodes labeled $(0,\kappa _1,\aleph _0)$ and $(0,\kappa _1,\aleph _1)$ , mean that $\leqslant _B$ is an injective but not surjective correspondence between the $\sim _B$ -classes of equivalence relations with such characteristic triples.

4 Comparison with equivalence relations on Polish spaces

This section determines all comparabilities between equivalence relations on Polish spaces and equivalence relations on $\omega _1$ .

Lemma 4.1 Let X be a Polish space and $f:\omega _1\to X$ . Then f is Borel if and only if there exists a thick set $C\subseteq \omega _1$ such that $f_{|_C}$ is constant.

Proof Suppose that f is Borel. If X is finite, then it follows immediately that f is constant on a thick set, so assume that X is infinite. For every $n\in \mathbb N $ , let $ {\mathcal B_n=\{ B_{nm}\}_{m\in \mathbb N }}$ be a partition of X into Borel subsets of diameter less than $ \frac 1{n+1} $ , and such that $ \mathcal B_{n+1}$ refines $ \mathcal B_n$ . Then there is a sequence $\{m_n\}_{n\in \mathbb N }$ of natural numbers such that $B_{n+1,m_{n+1}}\subseteq B_{nm_n}$ and $C_n=f^{-1}(B_{nm_n})$ is thick, for every $n\in \mathbb N $ . Therefore, $C=\bigcap _{n\in \mathbb N }C_n$ is thick and $f_{|_C}$ is constant.

Conversely, if C is a thick set such that f is constant on C, let x be the value taken by f on C. Then given $B\subseteq X$ it turns out that $f^{-1}(B)$ is either thin or thick, so Borel, according to whether $x\notin B$ or $x\in B$ .

Proposition 4.2 Let X be a Polish space, let E be an equivalence relation on $\omega _1$ , and let F be an equivalence relation on X. Then $E\leqslant _BF$ if and only if E has a thick equivalence class and .

Proof Let $f:\omega _1\to X$ be a Borel reduction of E to F. By Lemma 4.1, let C be a thick set on which f is constant. Then C is contained in a thick equivalence class of E. Moreover, as f is a reduction.

Conversely, if E has a thick equivalence class and , let $f:\omega _1\to X$ be a reduction of E to F constant on every equivalence class of E. Then f is Borel by Lemma 4.1.

Lemma 4.3 Let X be a Polish space, and let $\{ B_{\alpha }\}_{\alpha \in \omega _1}$ be a family of pairwise disjoint, non-empty Borel subsets of X. Then there exists $I\subseteq \omega _1$ such that $\bigcup _{\alpha \in I}B_{\alpha }$ is not Borel.

Proof If $\bigcup _{\alpha \in \omega _1}B_{\alpha }$ is not Borel, let $I=\omega _1$ . Otherwise, toward contradiction, deny the conclusion. Let $Y=\{ y_{\alpha }\}_{\alpha \in \omega _1}$ be a non-analytic subset of X of cardinality $\aleph _1$ , and let $g:\bigcup _{\alpha \in \omega _1}B_{\alpha }\to X$ be defined by letting $g(x)=y_{\alpha }$ for the unique $\alpha $ such that $x\in B_{\alpha }$ . Then g is Borel but has non-analytic range, a contradiction.

Lemma 4.4 Let X be a Polish space, and let $f:X\to \omega _1$ . Then f is Borel if and only if the range of f is countable and $f^{-1}(\{\beta \} )$ is Borel for every $\beta \in \omega _1$ .

Proof Assume that f is Borel. Then the preimage of every singleton is Borel. Toward contradiction, assume that the range of f is uncountable. By [KT2006, Chapter 20, Problem 25], there exists a thin subset B of the range of f such that $ \mathrm {{card}} (B)=\aleph _1$ . Then the preimages of singleton subsets of B form a family $\{ A_{\alpha }\}_{\alpha \in \omega _1}$ of pairwise disjoint Borel subsets of X. By Lemma 4.3, let I be such that $\bigcup _{\alpha \in I}A_{\alpha }$ is not Borel. Then $f[\bigcup _{\alpha \in I}A_{\alpha }]$ is thin, so Borel, while $f^{-1}(f[\bigcup _{\alpha \in I}A_{\alpha }])=\bigcup _{\alpha \in I}A_{\alpha }$ is not Borel, a contradiction.

Conversely, if the range R of f is countable and the preimage of every singleton is Borel, given any $B\subseteq \omega _1$ one has that $f^{-1}(B)=\bigcup _{\beta \in B\cap R}f^{-1}(\{\beta \} )$ is a countable union of Borel sets, so it is Borel.

Proposition 4.5 Let X be a Polish space, let E be an equivalence relation on X, and let F be an equivalence relation on $\omega _1$ . Then $E\leqslant _BF$ if and only if all equivalence classes of E are Borel and .

Proof Let $f:X\to \omega _1$ be a Borel reduction of E to F. By Lemma 4.4, the preimage under f of any subset of $\omega _1$ is Borel, in particular, all E-classes are Borel. The inequality holds as the equivalence classes of E are preimages of pairwise disjoint subsets of the range of f, while the inequality holds as f is a reduction.

Conversely, assume that all equivalence classes of E are Borel and . Let $\{ A_n\mid n<N\} $ be an enumeration of the equivalence classes of E, and let $\{\beta _n\mid n<N\} $ be a set of pairwise F-inequivalent elements of $\omega _1$ , for some $N\leqslant \aleph _0$ . Let $f:X\to \omega _1$ be defined by letting $f(x)=\beta _n\Leftrightarrow x\in A_n$ . Then f is Borel by Lemma 4.4 and reduces E to F by construction.